bike sharing predictions

code

The code is a single script (script/etl.py) that uses the library lernia for machine learning and albio

refrences

For the current assessment we sketch an analysis procedure and we refer to a more detailed documentation on similar past use cases:

convNet for time series

time series forecast

capture rate for restaurants

feature cleaning for weather prediction

weekly pattern recognition

forecastability on reference data

feature importance

assessment

First of all we visualize the time series

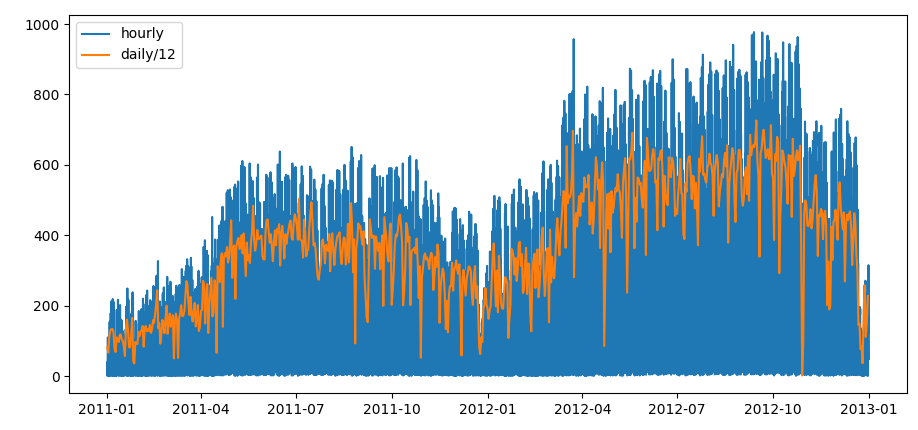time_series visualization of the time series for the hourly and daily resolutions

We than check data consistency:

check result
NaN 0
casual + registered == cnt yes
suspicious missing atemp 2
suspicious missing windspeed 2180
suspicious missing hum 22

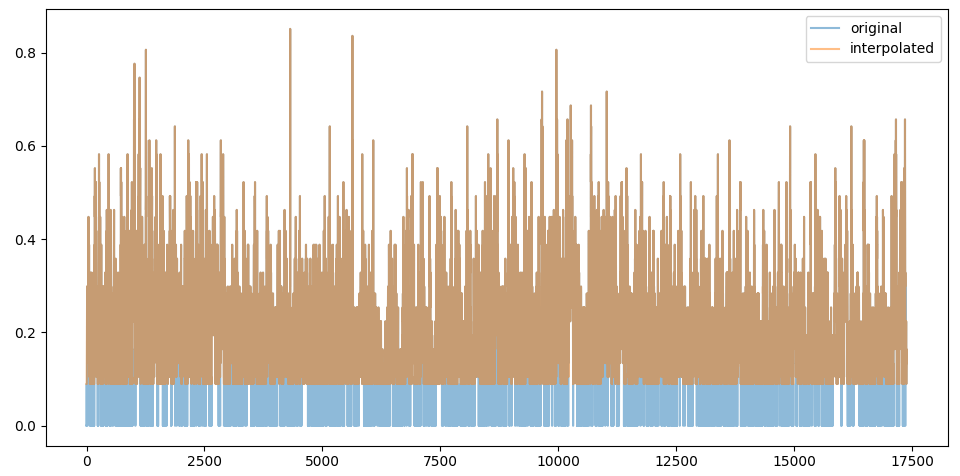interp_missing interpolating missing values for windspeed

The zero values for windspeed look like missing values, they represent 1% of the total values bu we decide to interpolate them nevertheless and we see that we slightly increase the overall correlation by replacing them.

feature classification

We classify the features into two groups, continuous and categorical for running different type of tsts. For the continuous variables we can perform regression, and calculate metrics like information gain, relative error, , correlation…

Continous features are: temp, atemp, hum, windspeed,weathersit

For categorical features we can’t suppose that the values are ordered. Even for weathersit we don’t know if the ordering is monotonously correlating with the outcome.

We can turn categorical variables into continuous by stretching intervals, resorting values or grouping categories (for example grouping saturday and sunday into weekend for the varaible weekday). But in these case we will treat categorical variables separately.

Categorical variables are: mnth, hr, holiday, weekday, season, weathersit

The outcomes of the problems are: casual, registered, cnt

continuous features

For continuous features we first calculate correlation to exclude the most obvious dependent features.

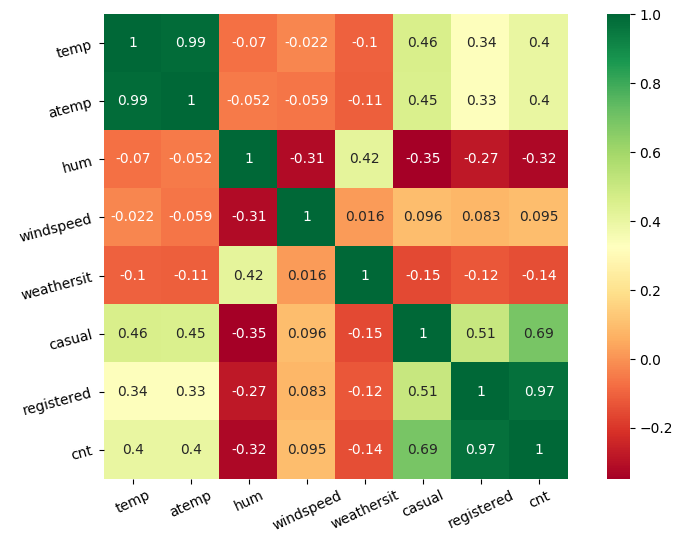corr_weather weather related features cross correlation

We clearly see that temp and atemp correlate and we keep atemp since contains more information(air humidity, windspeed…).

Since


cnt = registrated + casual

features correlate 100%, so we discard registered since is linearly dependent from the other two variables.

We don’t spot any other relevant correlation but we understand that humidity is a good predictor and most probably windspeed is not a good predictor and can be described by atemp and hum.

categorical feature sub sampling

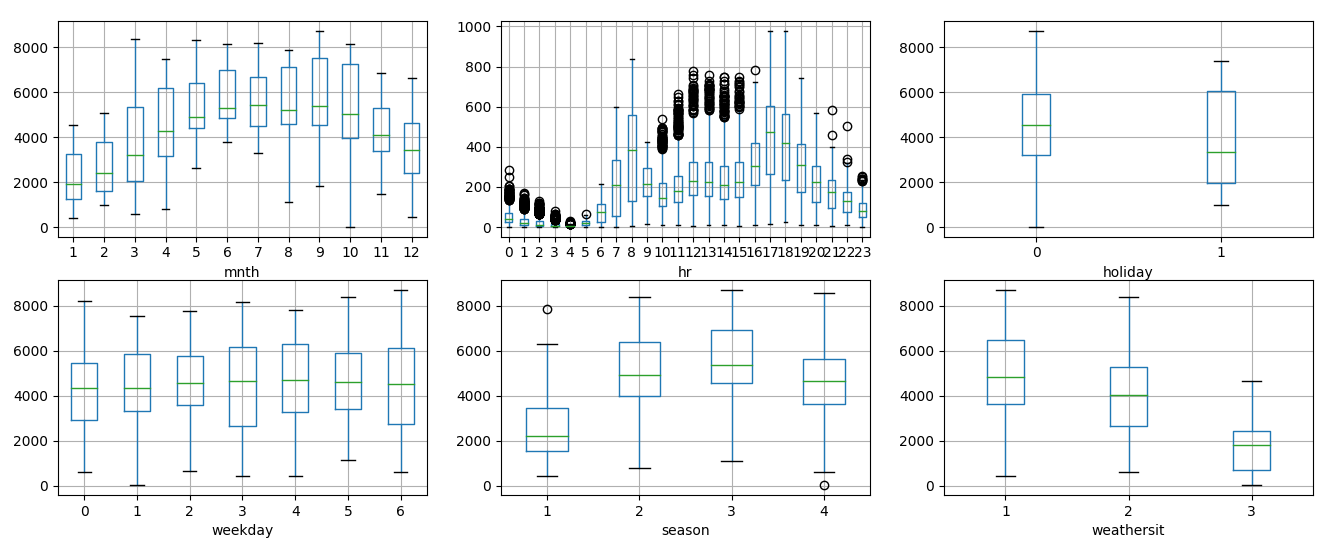
We check how categorical variables might subset the total count and we display the boxplot on the time variables

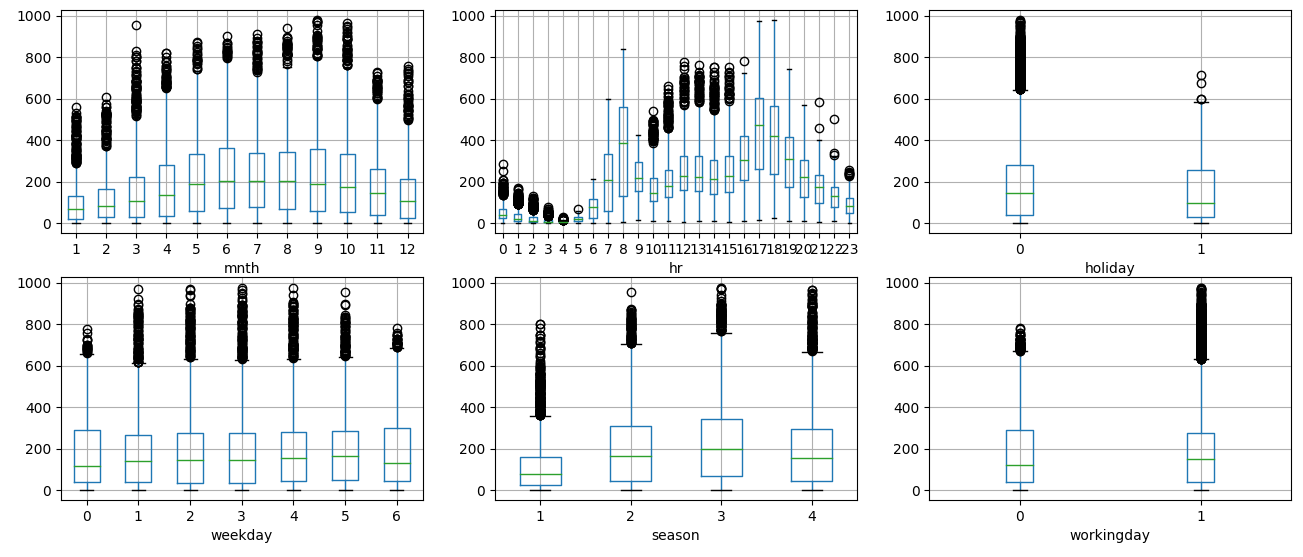time boxplot boxplot of cnt depending on time variables

We see that out of seven time variables only hr shows significant difference in counts, while the other variables show a light dependence on time.

boxplot_daily boxplot of cnt depending on time variables, daily values

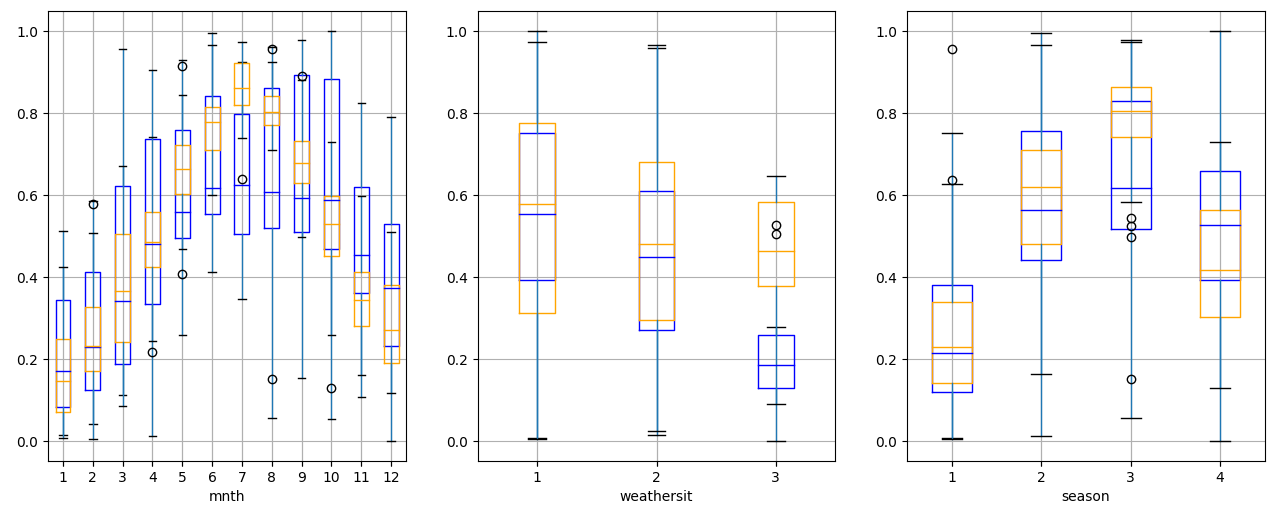
Looking at the daily values we remove fluctuations and we see a clearer dependance with season and month

On the other side we can imagine how season and month correlate with temperature.

temp_time temperature (orange) and counts (blue) divided by time

Which means that the most information about the seasonal influence on counts is conveyed by temperature

aggregate variables

Using hum, atemp, windspeed we can predict weathersit with 0.7 correlation.

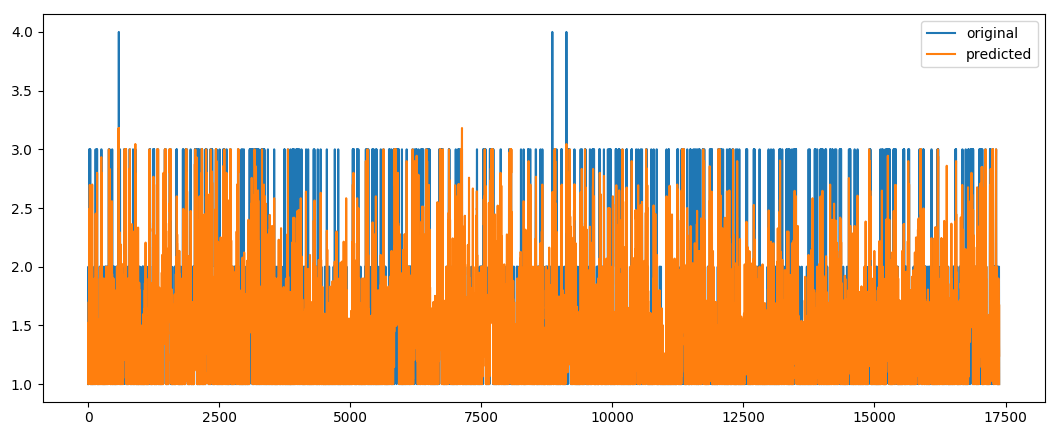prediction weather prediction of weather situation

Correlation is not high because cloudcover is not present.

weathersit is not well defined because values are bad distributed

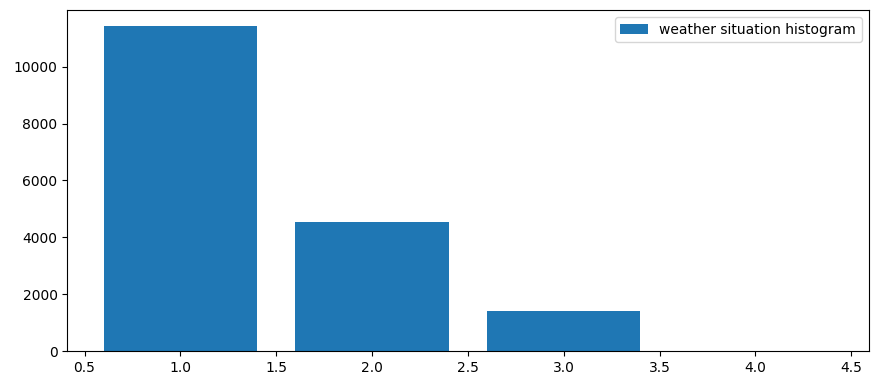histo_weathersit istogram weathersit

We than decide to not use it as predictor.

variance analysis

An important sign for predictor strenght is the variance analysis. We normalize the variables and display the variance.

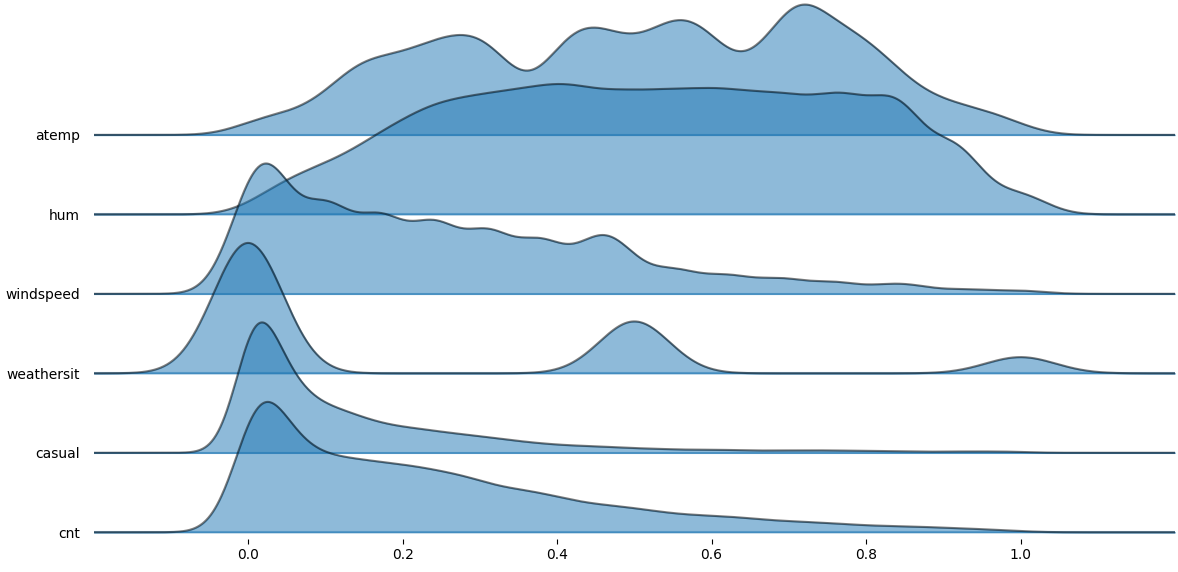variance_dist variance distribution

Big and small variances have bad prediction strength.

regression coefficients

A different selection of features changes the relative weights.

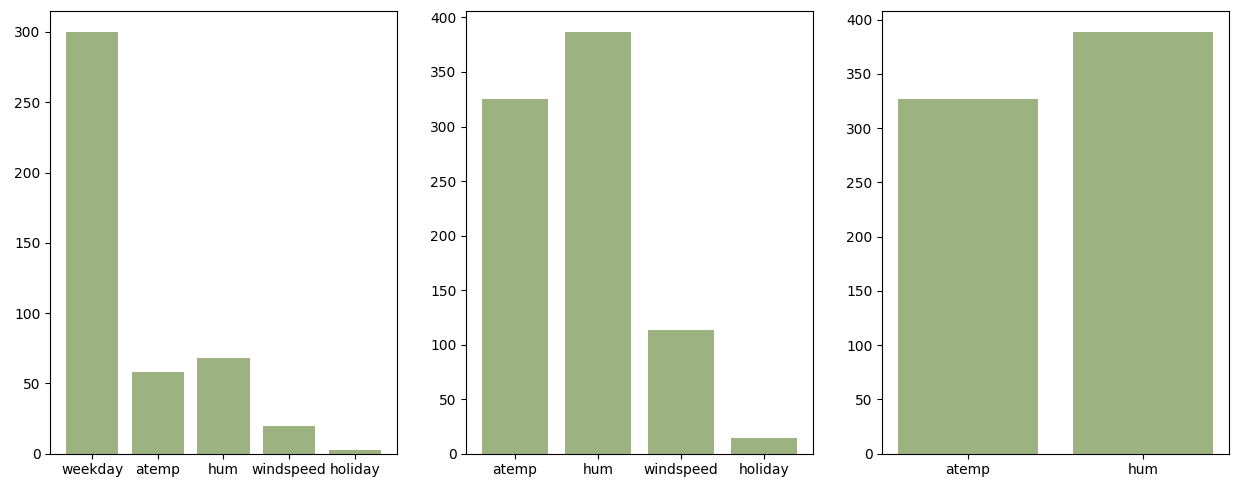reg_coeff regression coefficients

daily prediction

We use a bagging regressor with an 6-fold cross validation taking random samples out of the series.

If we use atemp and hum we can predict cnt with reliable accuracy

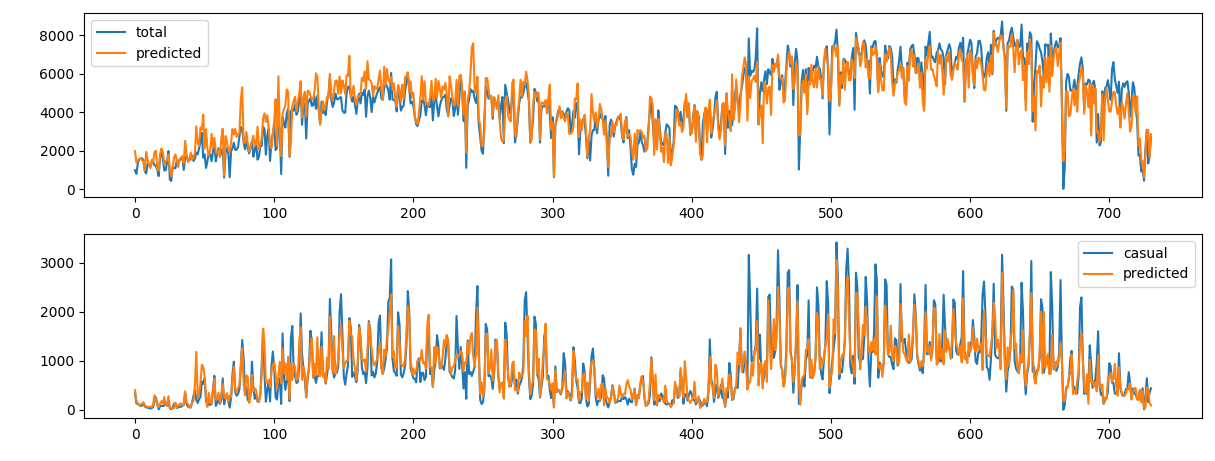cnt_pred count prediction on daily values

outcome features correlation relative error
cnt 2 0.91 12 %
casual 2 0.87 24%
cnt 4 0.92 12 %
casual 4 0.94 15%

Adding weekday and holiday improves only the performances for casual customers which is expected since recurrent customers have a more stable pattern.

The regular structure is easily predicted by the regressor.

hourly prediction

To predict the hourly values we divide the daily sum by the hourly split and have a regular pattern to predict. We remove weather features and train with hr, weekday, and holiday.

We do a 10-fold cross validation with the same bagging regressor.

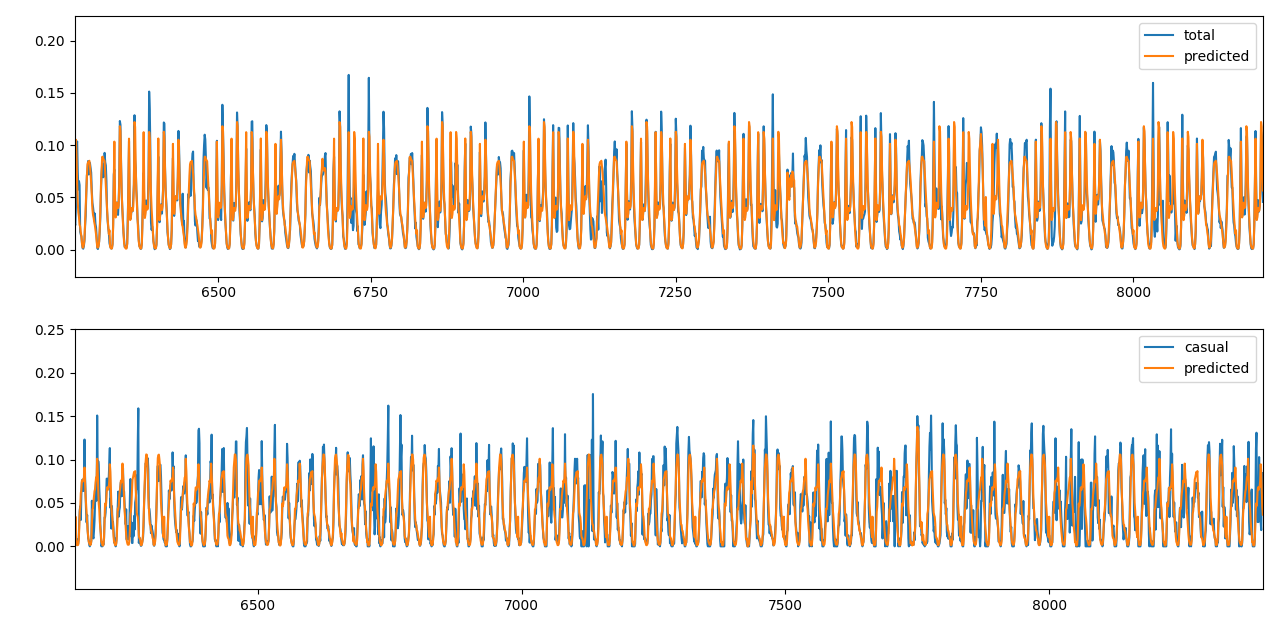cnt_pred count prediction on hourly values

outcome features correlation relative error
cnt 3 0.92 15 %
casual 3 0.83 29%

If we pipe together the two predictions we achieve good correlation and acceptable relative error.

outcome features correlation relative error
cnt 3 0.92 23 %
casual 3 0.91 30%

half day forecast

To forecast half of the remaining day we sum only the first 12 h of the day to predict the daily values.

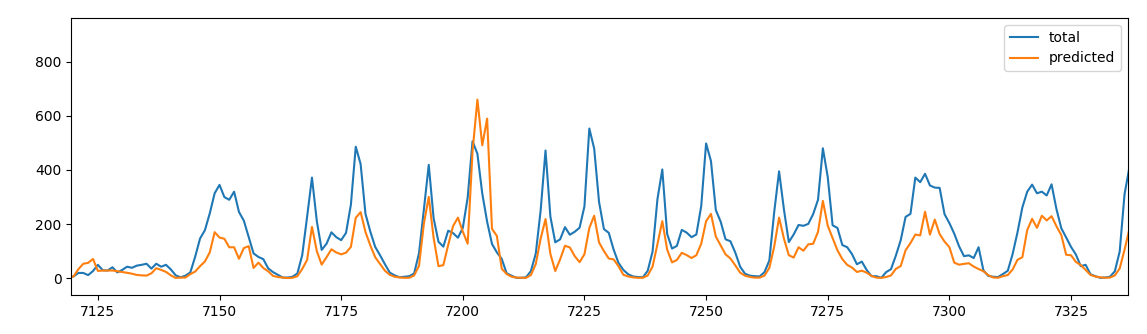cnt_pred prediction with half day info

outcome features correlation relative error
cnt 3 0.79 60 %

We can further improve the results calculating the correct ratio between the two parts of the day and perform a separate prediction for the two half of the day.