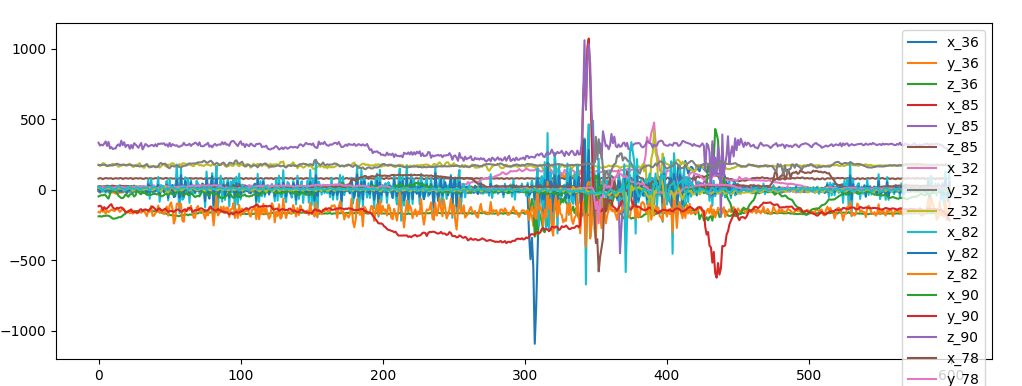
 superposition of sensor data for accellerometer
superposition of sensor data for accellerometerIn raw/ there are csv files with time series data of inertial sensors installed in a car:
Which we load with this script.
 superposition of sensor data for accellerometer
superposition of sensor data for accellerometer
Without further information (timestamp and position of the sensor) we can't assume that sensors are alligned in space and synced.
Still sensors might be aligned:
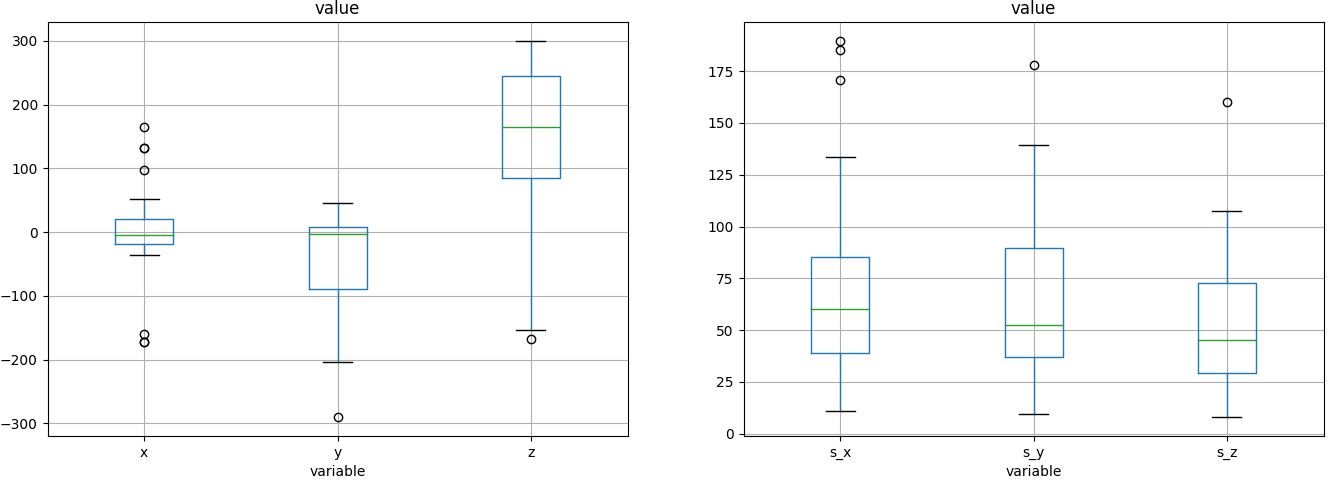 similar acceleration between sensors
similar acceleration between sensors
We can suppose that y adds gravity, z is the direction of motion and x is the lateral displacement and we can reconstruct the equation of motion and see that the car is accellerating (probably we should remove the constant gravity).
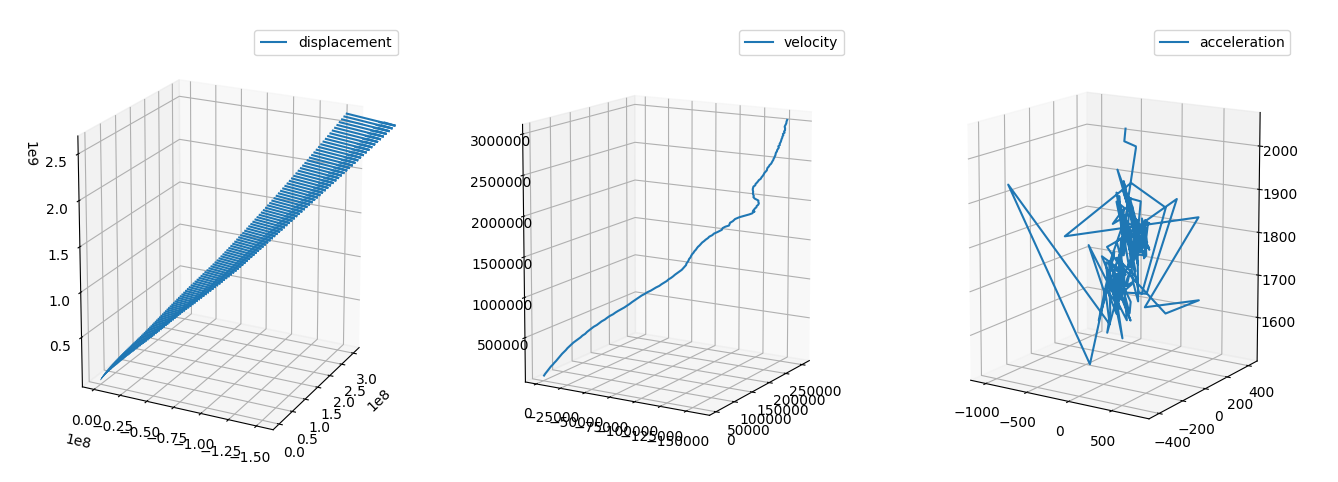 equation of motion
equation of motion
To capture the most essential feture of a time series we first smooth and calculate the derivatives of the time series.
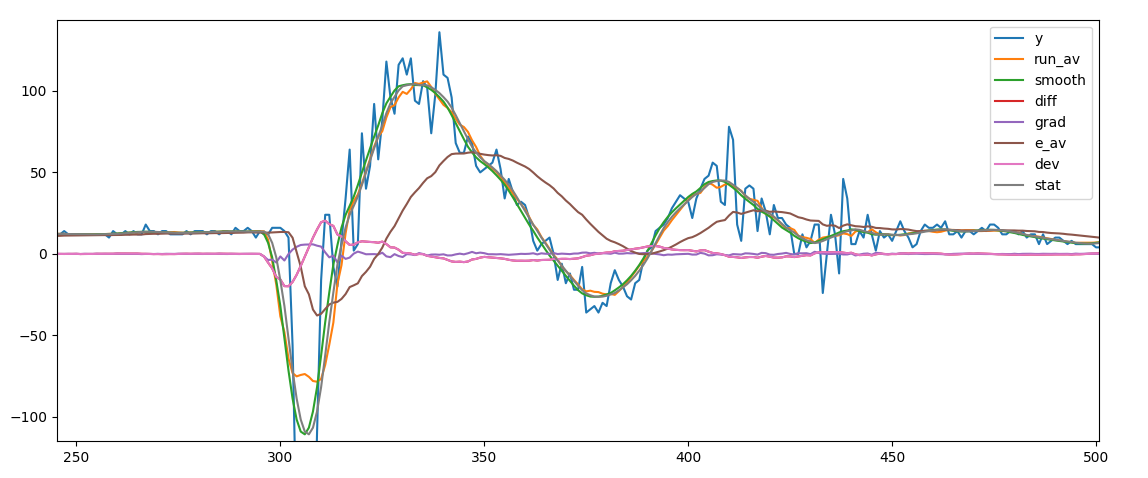 smoothing of the series
smoothing of the series
The single series are calculated as follow:
serD = pd.DataFrame({'y':y})
serD.loc[:,"run_av"] = serRunAv(y,steps=period)
serD.loc[:,"smooth"] = serSmooth(y,width=3,steps=period)
serD['diff'] = serD['smooth'] - serD['smooth'].shift()
serD['grad'] = serD['diff'] - serD['diff'].shift()
serD['e_av'] = serD['y'].ewm(halflife=period).mean()
serD['stat'] = serD['run_av'] - serD['diff']Kaiser window smoothing delivers more stable results but running average is computationally more efficient. Derivaties are as well computationally really efficient (float difference).
After smoothing we can sample the signal (i.e. take every 3rd)
We analyze at first every single sensor independently and we classify the events
Since we have smoothed the signal we keep every third data point to reduce the size of the learning set. We create a series of segments chopping the signal into sequential windows of 16 data points.
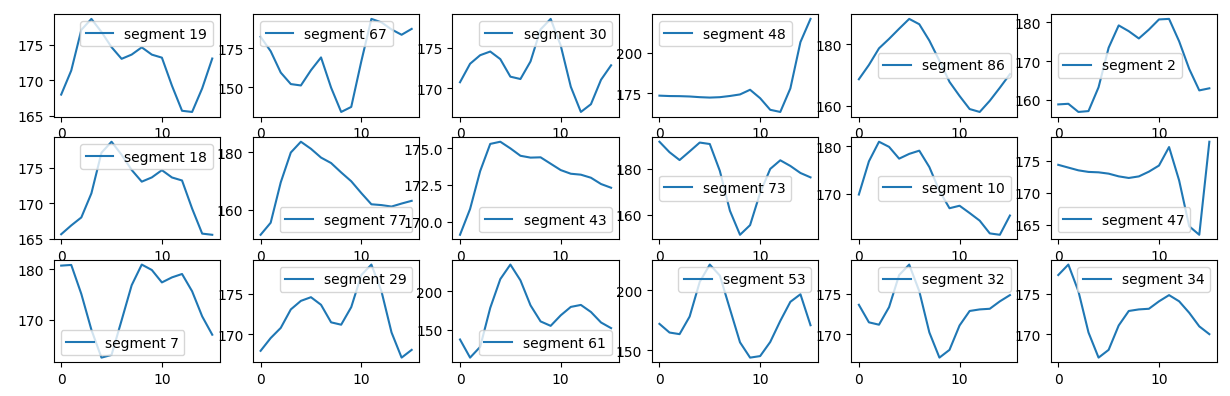 training set for unsupervised shape classification
training set for unsupervised shape classification
We use sklearn kmeans cluster to clusterize the shape.
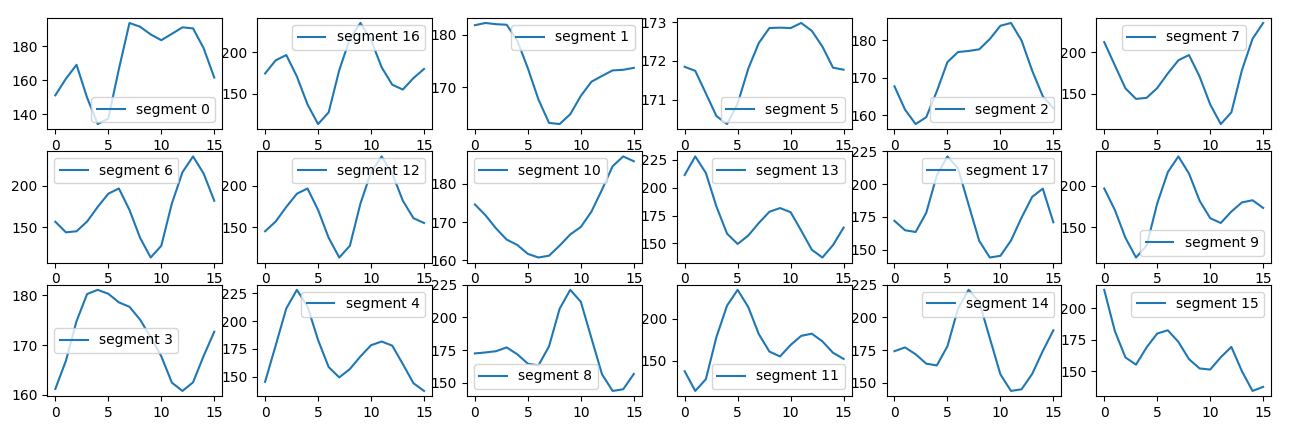 set of shapes from the k-means fit
set of shapes from the k-means fit
Each cluster should have a physical meaning and can be ad hoc adjusted
Each time series is now represented by a string of k-clusters:
We see in some cases an high correlation between clusters which mean we can reduce the size of k.
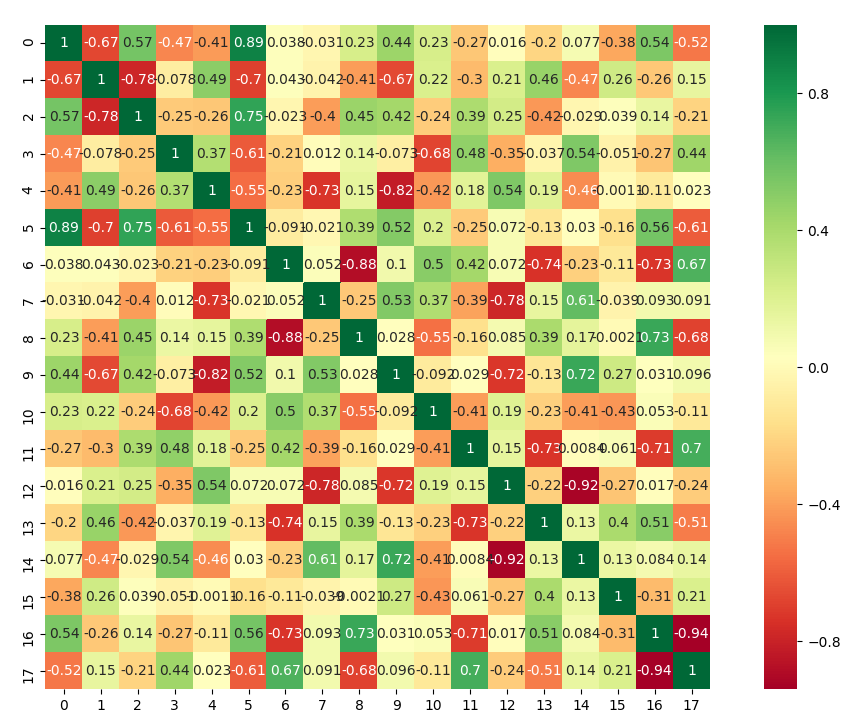 high correlation or anticorrelation between some clusters
high correlation or anticorrelation between some clusters
We can than evaluate in which cluster each segment belong
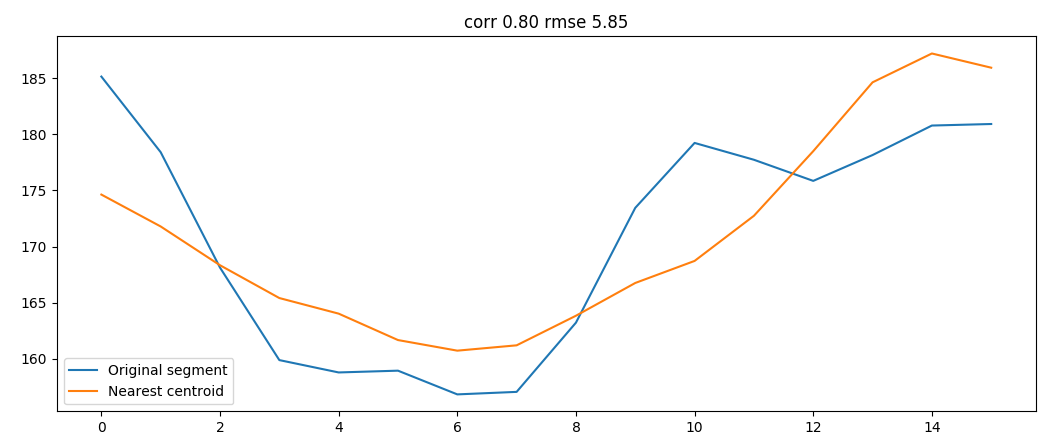 original segment and correspondent cluster
original segment and correspondent cluster
We can than reduce a window into a single class saving a lot of information
The power spectrum can with few data points convey many important information
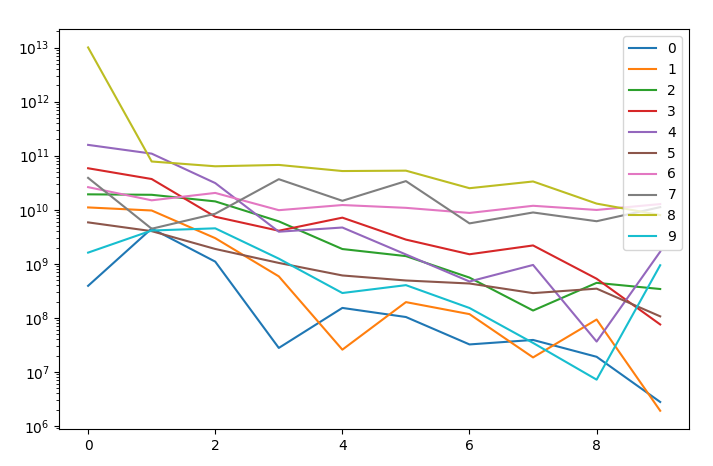 comparison of the power spectrum of few signals
comparison of the power spectrum of few signals
There is a strong correlation between many sensors
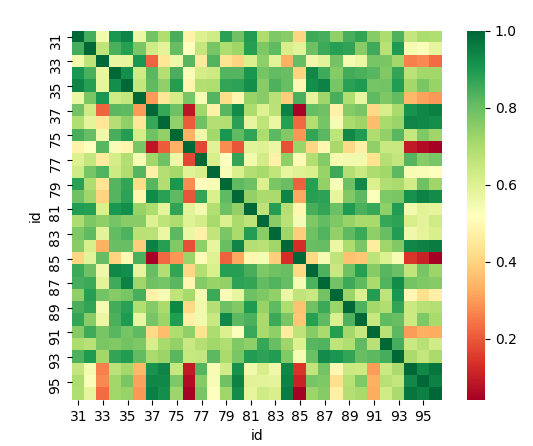 many sensors are higly correlated
many sensors are higly correlated
If we consider each direction taken separately we obtain a lower correlation which might reveal that some sensors might be flipped.
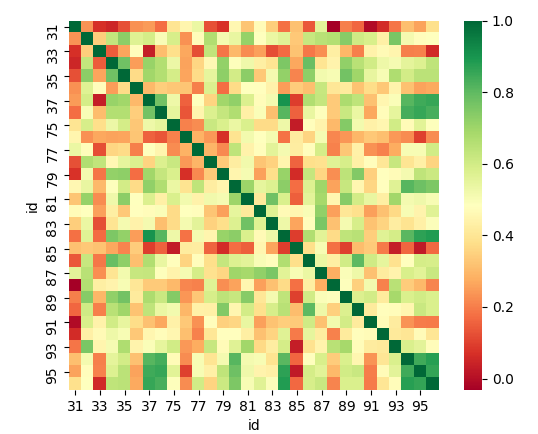 correlation from power spectrum, sum of directions
correlation from power spectrum, sum of directions
Power spectrum helps against redundancy
Power spectrum is an heavy computation and can be done at best in the communication design.
A similar analysis might be done with other statistical features of a sensor:
Further statistical properties should be added since the correlation matrix doesn't show useful interpreting results
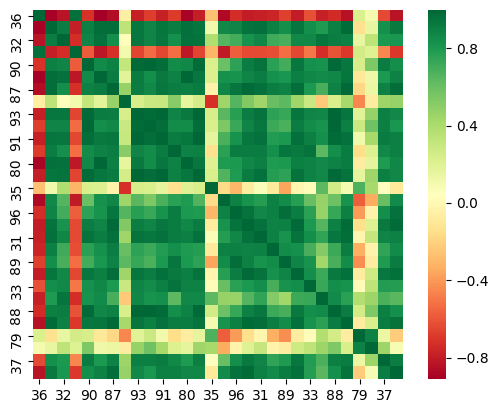 correlation of statistical properties
correlation of statistical properties
Once we establish a correlation between sensors we can build a graph and understand how to simplify the information across the system
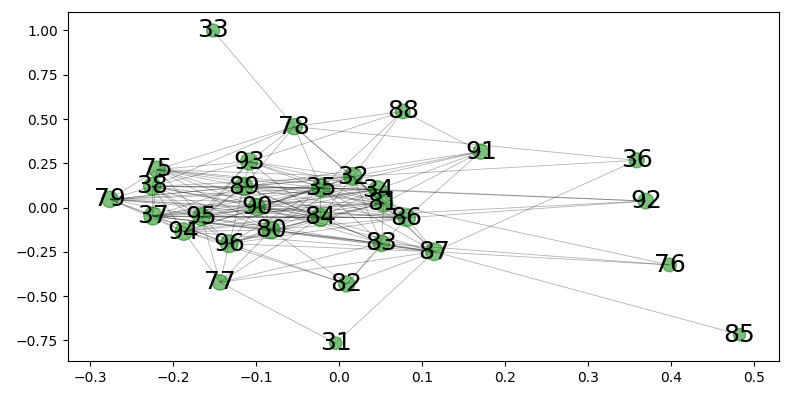 network from directional spectrum
network from directional spectrum
Different analysis lead to different results
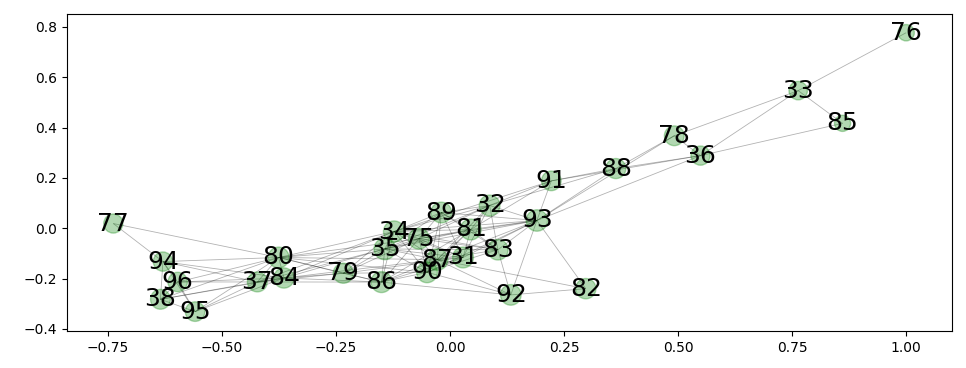 network from radial spectrum
network from radial spectrum
Depending on the functionality of the sensor we can decide to report only spikes using derivatives and callback functions.
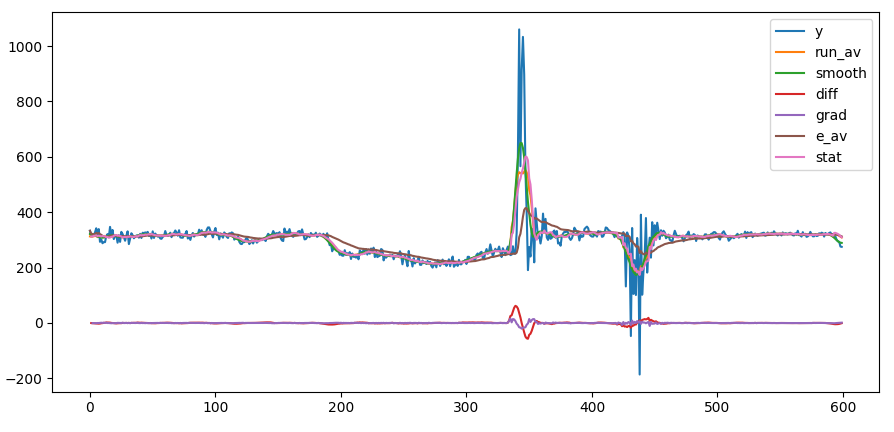 the derivative of the accelleration as spike
the derivative of the accelleration as spike
Derivaties should trigger a window and the event classification letting the sensor just send a single category + timestamp.
For this particular exercise we want to derive from the power spectrum the presence of a spike.
We first build a spike detector
y = sen[l].values
serD = s_l.serDecompose(y,period=16)
serT = s_l.serDecompose(serD['diff'].abs(),period=16)
spik = serT['smooth'].values > np.mean(serT['smooth'])*3.and we than create the training set
feat = psPx.T.sort_values('id')
spik = spL.sort_values('id')['x'] > 0
X = feat.values
y = spik.values * 1We than use the two methods mentioned in the assignement (support vector classifier - sklearn, neural network - keras) and compare the performances:
Neuronal network with the given topology are much slower and less performant than support vector machine. I some cases the network get trapped in a local minimum and does not find the solution.
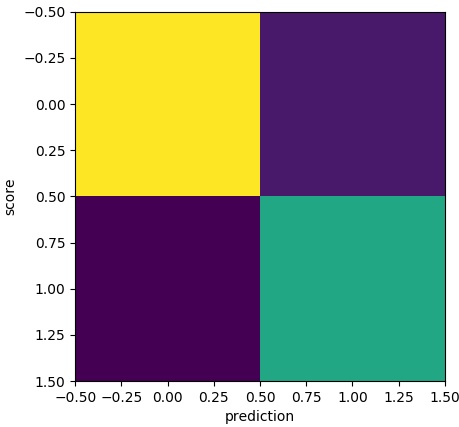 confusion matrix for the neural network when trapped in a local minimum
confusion matrix for the neural network when trapped in a local minimum
We want to understand which is the learning capability of a cluster of sensors to create local processing nodes which summarize the information.
Since convolutional neural networks are really performant we transform our time series into images usinig a characteristic period (from power spectrum)
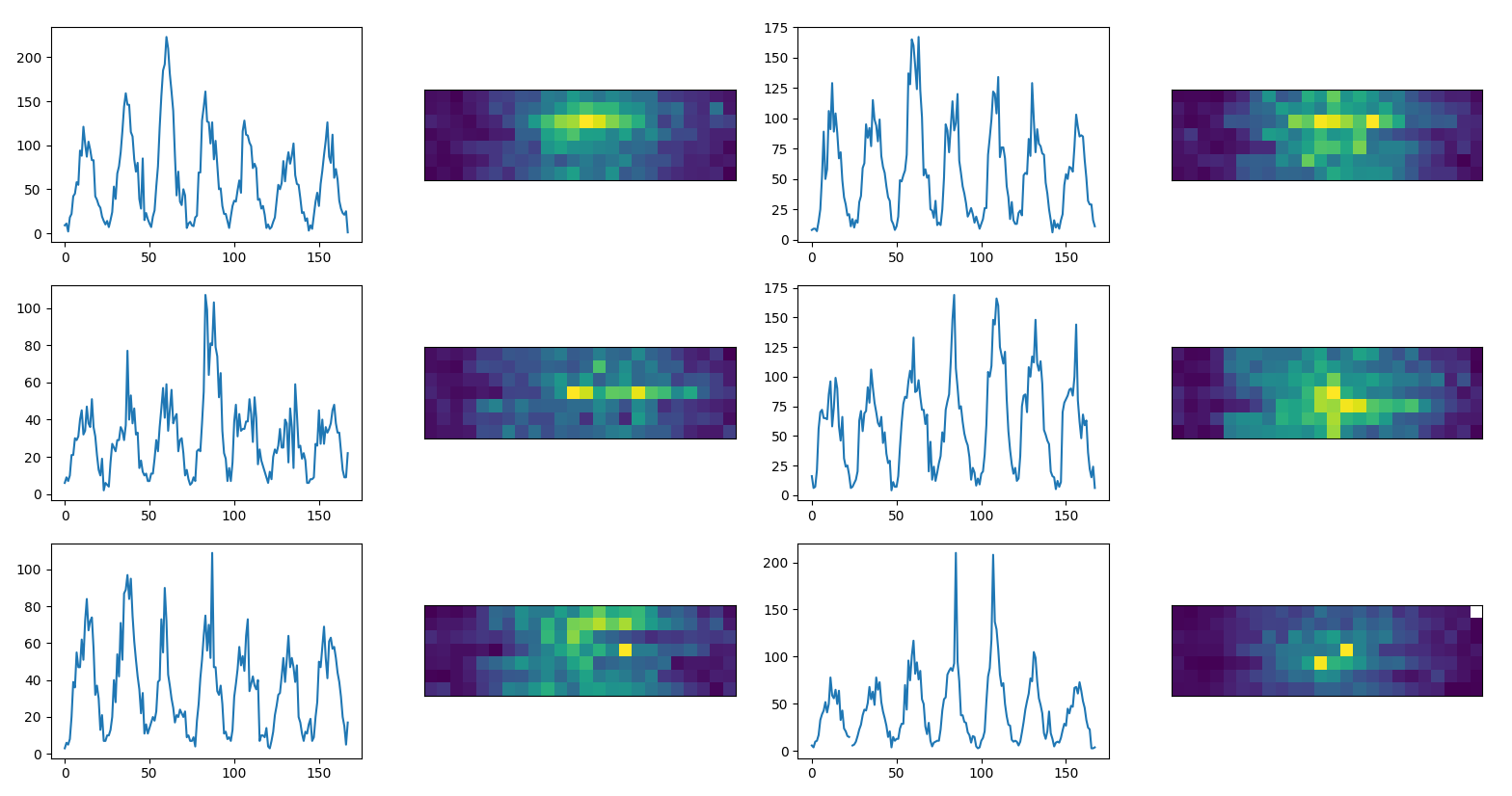 time series as images (example data)
time series as images (example data)
and we write an autoencoder to predict each image and calculate performances
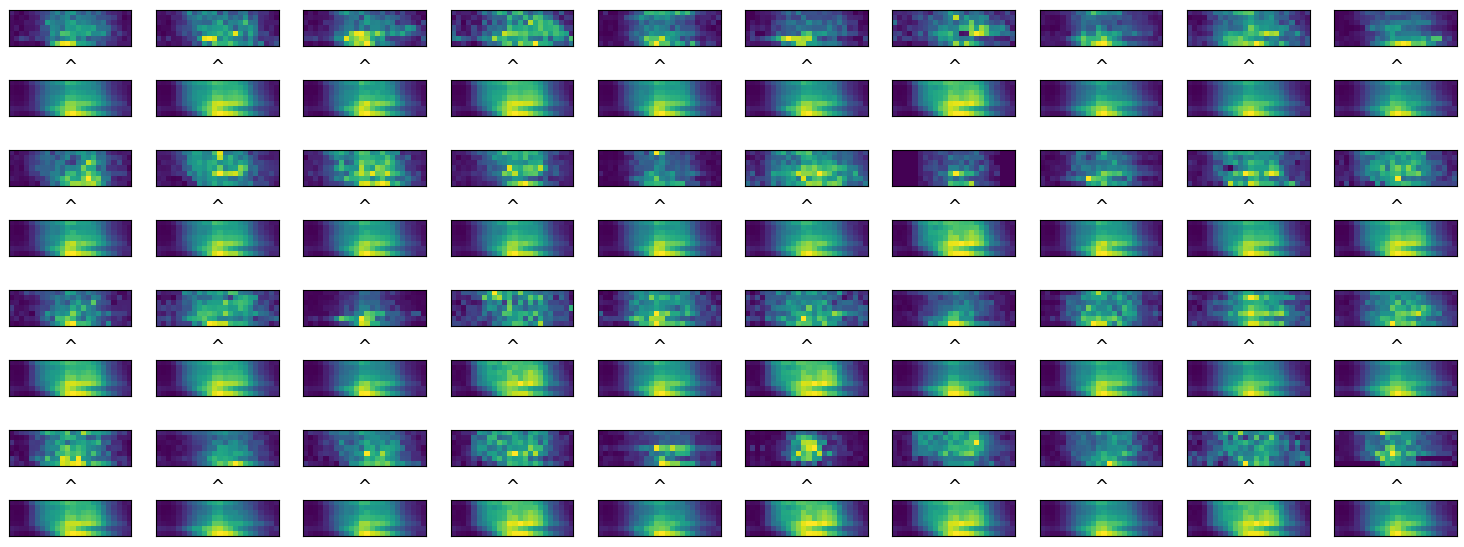 comparison between original time series and their predictions (example data)
comparison between original time series and their predictions (example data)
We take a set of sensors into a cluster node and we predict one time series with the help of the others
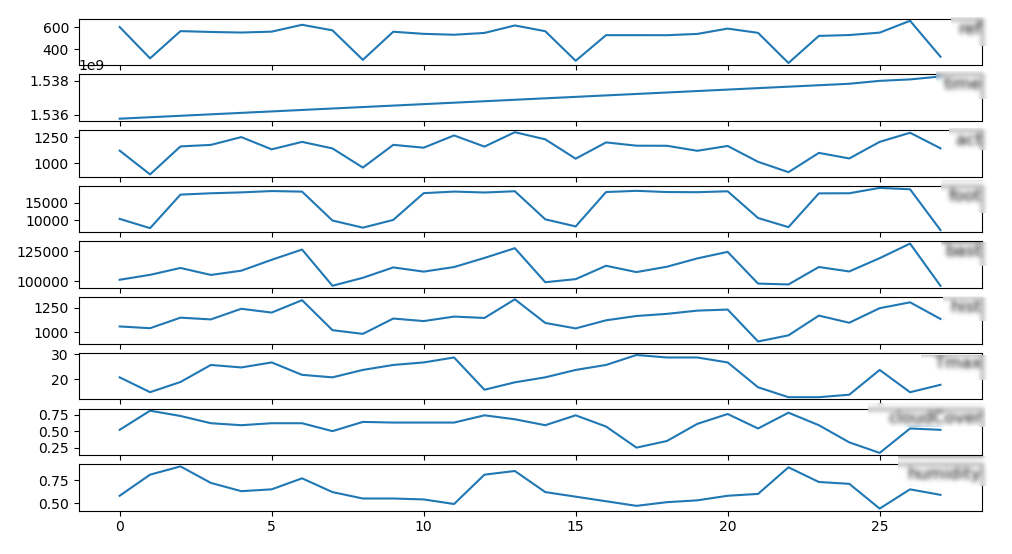 series of data for learning (example data)
series of data for learning (example data)
We than perform a long short term memory learning with keras and study the influence of each sensor into the prediction
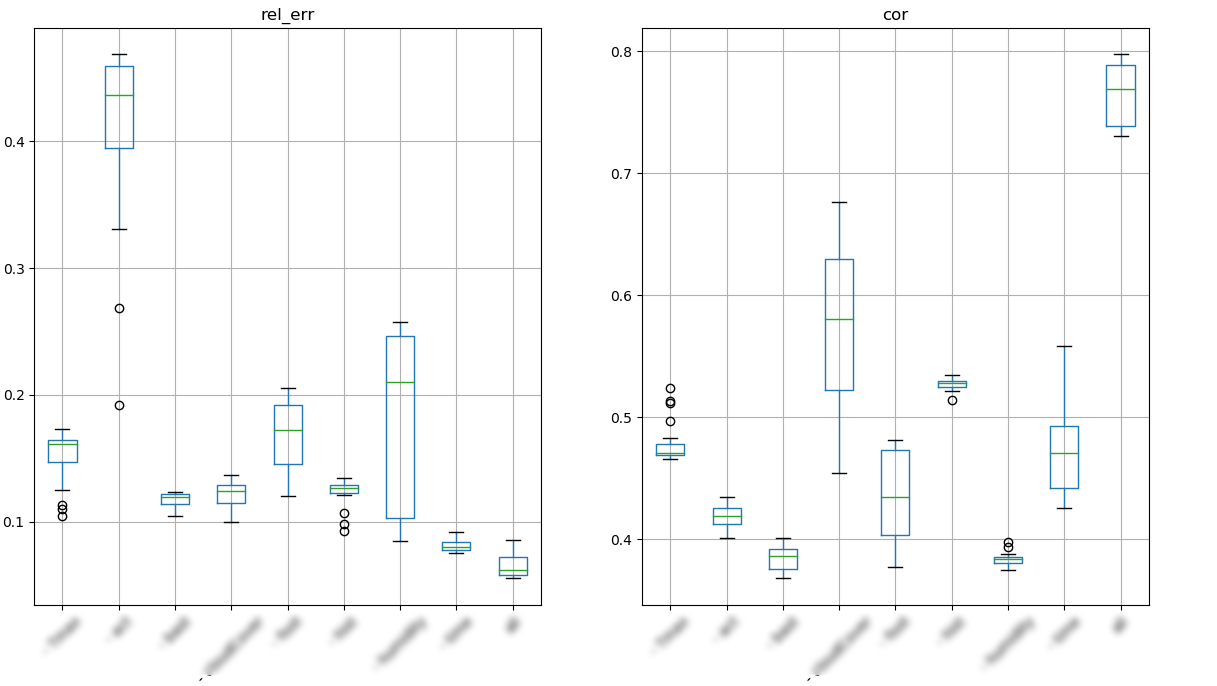 performances on predictions after feature knockout (example data)
performances on predictions after feature knockout (example data)
There are different algorithms that can be tested for classify the signals. Among the most interesting we point to:
There is a list of further analysis to do to investigate further information in the system:
Part 2
sklearn provides an api and doc for dictionary learning.
Now we have time series expressed as strings and we want to: * Finds a dictionary (a set of atoms) that can best be used to represent data using a sparse code.
Given goal (b) in the context of a sparse coding problem:
You may use sklearn Dictionary Learning for the sparse coding part. Which other tools/methods would you suggest?
A Kernel function K in support vector machine acts like an inner product in a transformed space 1 2 3 4 5
K(x, x′) = <ϕ(x),ϕ(x′)>
The number of parameters depend by the augmented dimensionality induced by the kernel. In case of a linear kernel ϕ can be expressed with a N number of parameters, for non linear kernels it depends whether we use a polynomial, gaussian, or gaussian radial kernels 6.
In general the kernel acts in a M-dimensional space operating on the N features, where M > N, to find a linear classification in the M dimensional space.
From sklearn we can extract the attributed of the kernel
We create a fully connected network (no drop out) with 3 layers:
from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add(Dense(10, input_shape=(20,), activation='relu'))
model.add(Dense(5, activation='relu'))
model.add(Dense(1, activation='sigmoid'))We can then complile the model and test different optimizer and loss functions:
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])In our specific case we try as well this other combination
from keras.utils import to_categorical
y_binary = to_categorical(y)
model = Sequential()
model.add(Dense(10, input_shape=(20,), activation='relu'))
model.add(Dense(5, activation='relu'))
model.add(Dense(2, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y_binary, epochs=150, batch_size=10)
y_pred = np.array(model.predict(X) > 0.5)[:,1]
print(sum( abs(y*1-y_pred*1) ) )We see that both models sometimes get trapped in a local minimum and still don't perform as much as support vector machine which in few milli seconds always get to the correct solution.
You are given two strings. Write a Python function which would check if one of them can be obtained from the other simply by permutation of characters. The function should return True if this is possible and False if it is not possible. Example: for the pair (“qwerty”, “wqeyrt”) it should return True and for the pair (“aab”, “bba”) it should return False.
import string
def isPermuted(w1,w2):
cL = [c for c in string.ascii_lowercase]
d1, d2 = {}, {}
for c in cL:
d1[c], d2[c] = 0, 0
for w in w1.lower() :
d1[w] = d1[w] + 1
for w in w2.lower() :
d2[w] = d2[w] + 1
return d1 == d2
print(isPermuted("qwerty", "wqeyrt") )
>>> True
print(isPermuted("aab","bba"))
>>> False