visits vs activities

Our customer knows how many sales receipts are issued with an hourly resolution over around 400 gas stations in the country.

We call the reference data visits and our measured data activities.

Skews

To map activities into visits we have to correct different skews:

1. homogenity missing values
2. hourly phase shift
3. volatility big fluctuations
4. learning capability trainable locations
5. holiday tail effects
6. missing sources partial missing data
7. extrapolation factor for motorway drivers
8. market share business phone users on the motorway
9. weather influences motorway behaviour
10. commuter vs touristic road segment traffic per week day
11. population density high populated areas show large deviations
12. directions distinction uncertanty
13. distance filter optimal configuration
14. low counts lower precision
15. type of device road segment dependent
16. people/car vs people/receipt who is driving, who is paying

Project references

The project considers the following quantities:

The customer expectation are summarized in 4 KPIs:

distribution of daily visits

Raw data

Raw data consists in numbers of receipts per hour per location. We present the data week per week to show the differences between locations:

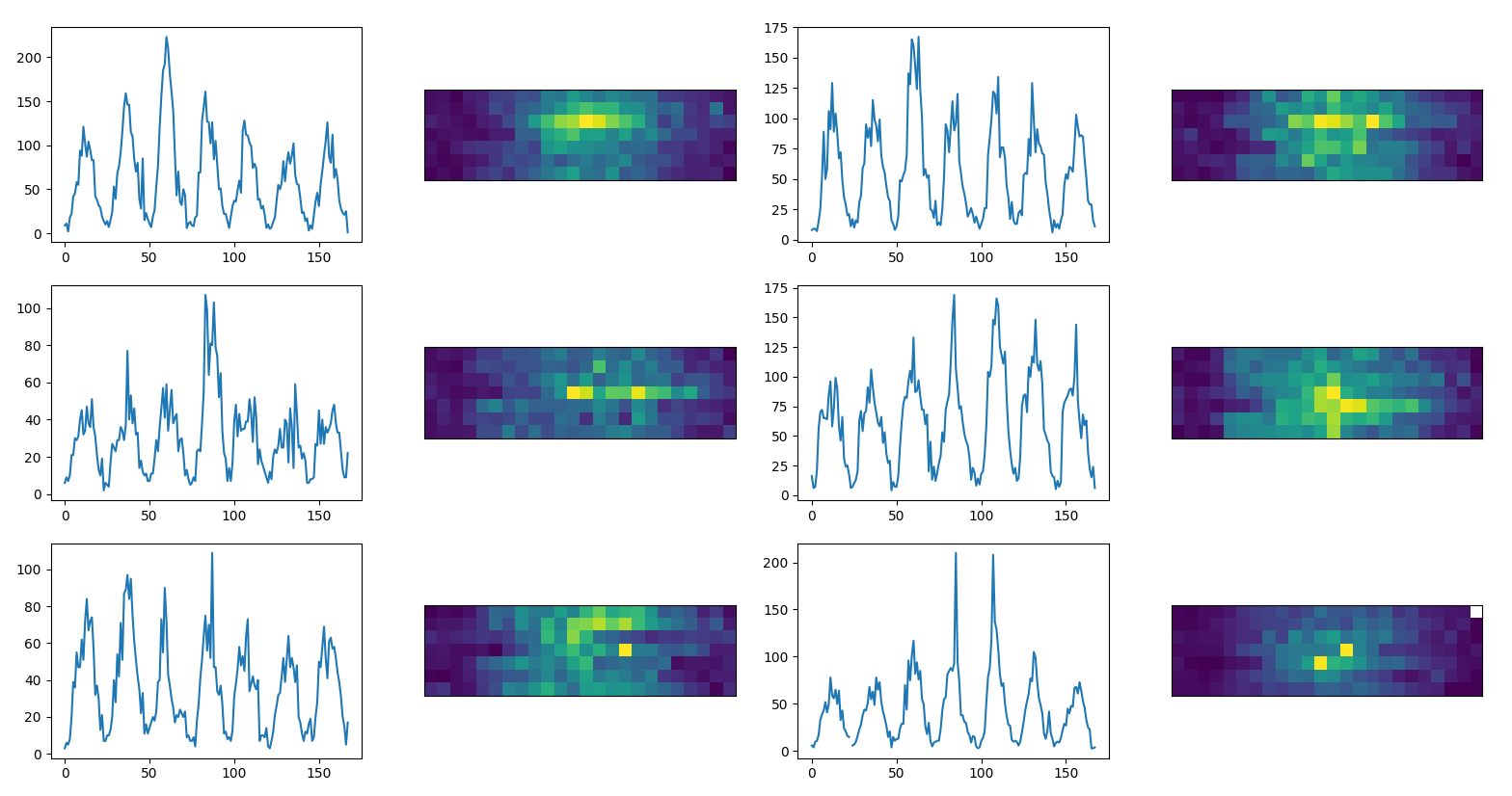reference time series, each panel present a different location and a different week. A week is represented as an image of 7x24 pixels

Locations show different patterns about daily and weekly peaks. Sometimes deviations between two days or two hours are really strong.

Skew I - homogenity

missing values

We homogenize the data converting the time series into matrices to make sure we have data for each our of the day. We than replace the missing values interpolating:

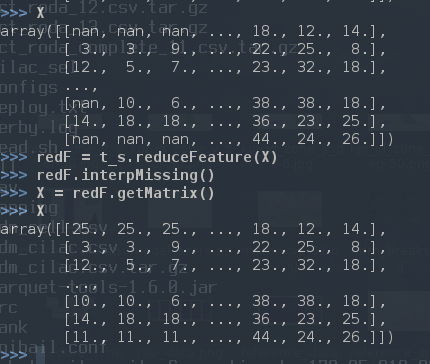replace missing values via interpolation

Skew II - hourly

smoothing

In order to compensate the effects of time shifting (can counts double within two hours?) we apply a interpolation and smoothing on time series:

to the raw reference data we apply: 1) polynomial interpolation 2) smoothing

Skew III - volatility

chi square distribution

Some locations are particularly volatile and to monitor the fluctuations we calculate the χ² and control that the p-value is compatible with the complete time series. We substitute the outliers with an average day for that location and we list the problematic locations.

Distribution of p-value from χ² for the reference data

We than replace the outliers:

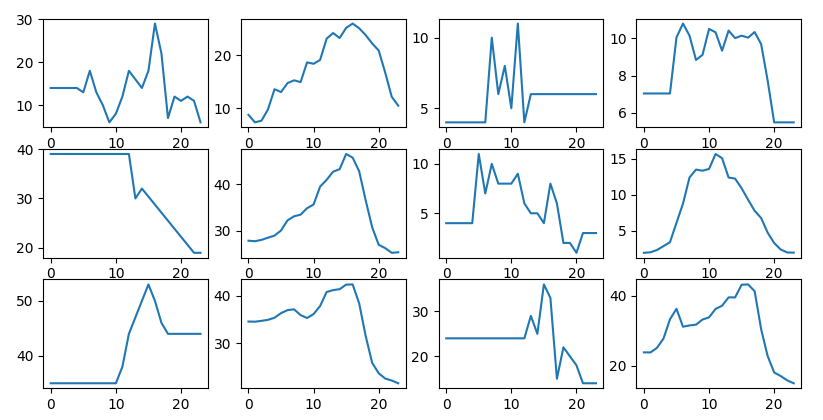outliers are replaced with the location mean day, left to right

Skew IV - learning capability

deep learning autoencoder

We build an autoencoder which is a model that learns how to create an encoding from a set of training images. In this way we can calculate the deviation of a single image (hourly values in a week 7x24 pixels) to the prediction of the model.

sample set of training images, hourly counts per week

In this way we can list the problematic locations and use the same model to morph measured data into reference data.

We train a deep learning model on images with convolution: sketch of the phases of learning

We than test how the images turn into themselves after the prediction of the autoencoder.

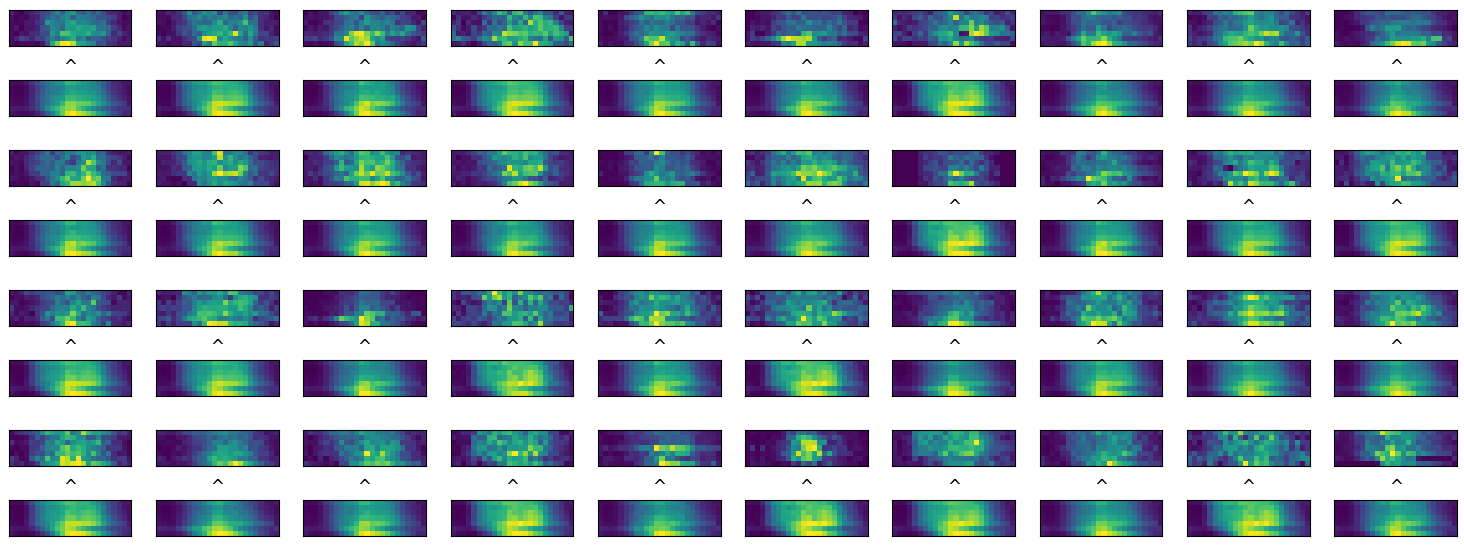comparison between input and predicted images

We can than state that 88% of locations are not well predictable by the model within 0.6 correlation. 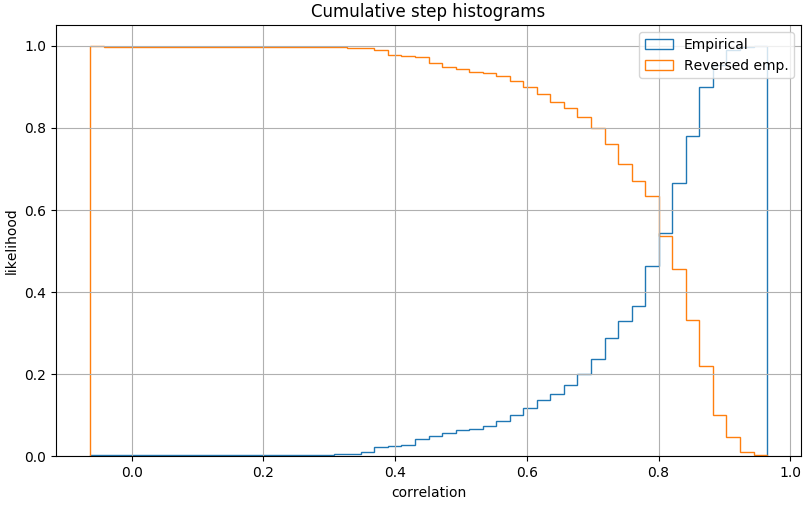distribution of correlation for autoencoder performances: correlation on daily values

Skew V - holiday

Holidays have a huge effect on customer side. The plot shows activities and visits for the month of March, the last Thursday of the month prior to easter shows a huge variation only on reference data.

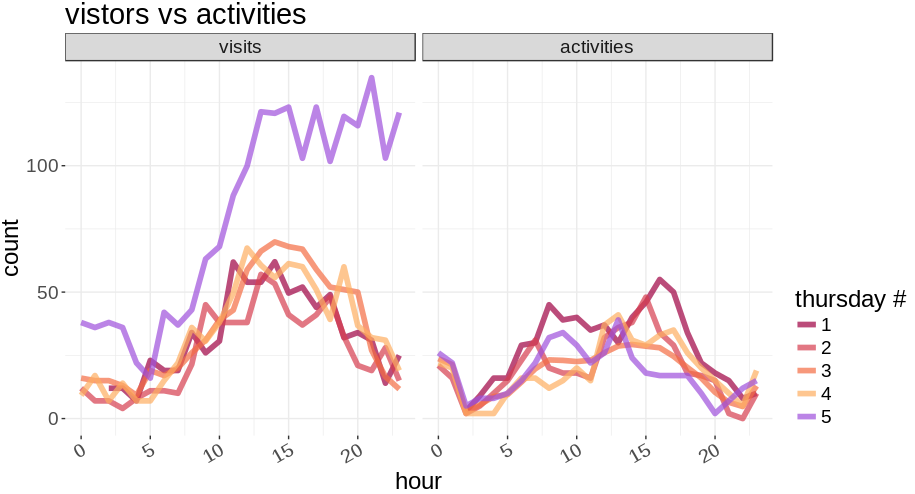Visits versus activities in Mach approaching easter

The same effect was seen in March 2017 in the test data. 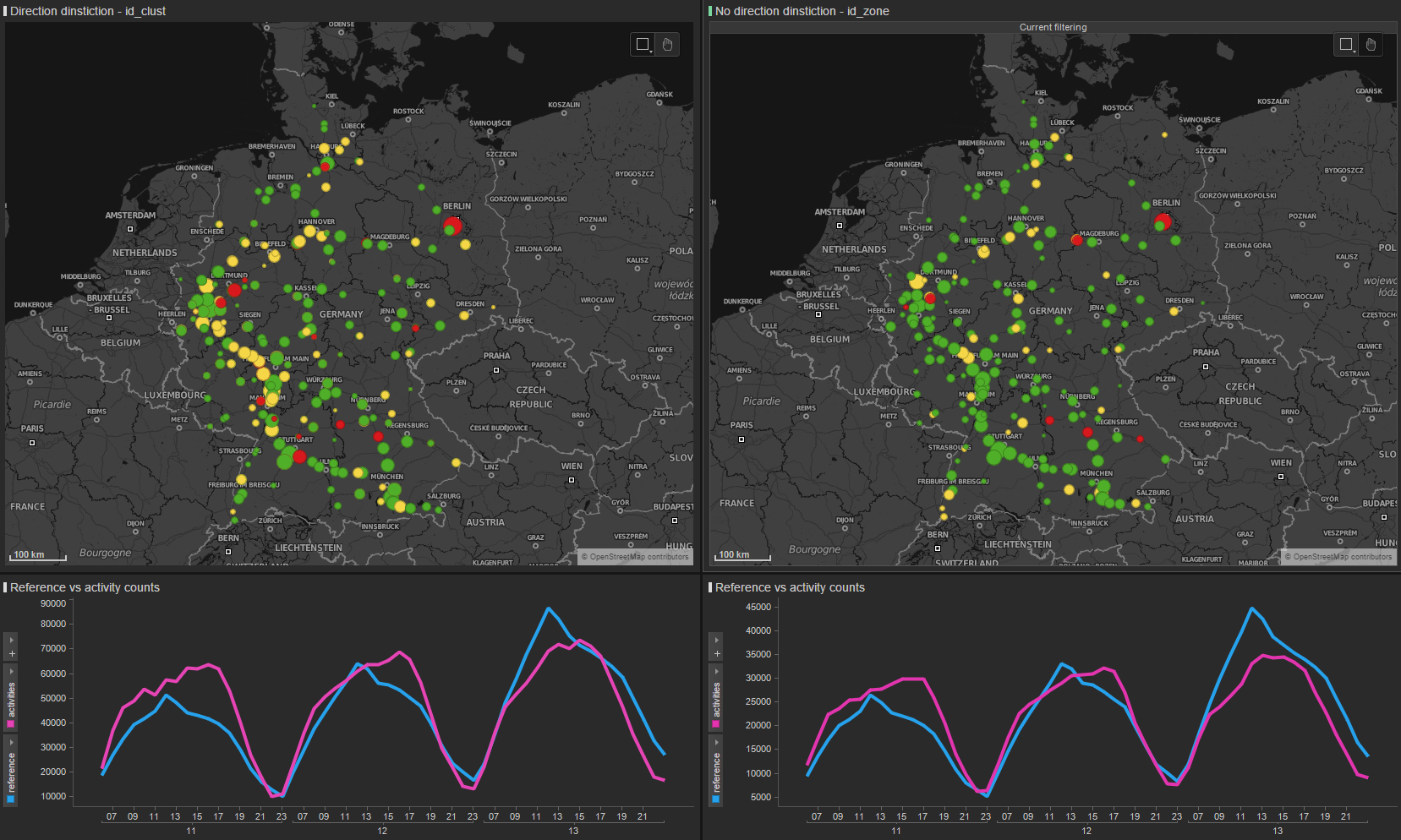Easter effect is visible only on reference data, blue line

Skew VI - missing sources

Gas stations are sometimes composite, we don’t receive complete information about all the visits in the area.

in same cases we don’t know the receipt counts for some buildings on the gas station

Skew VII - extrapolation factor

We should consider which extrapolation factor has to be used for motorway drivers:

1. first signal wrong in case of drivers sleeping in a hotel
2. local share wrong for long distance drivers
3. daily fluctuations dependent on road type
4. high density areas induce a bias

Some road segments have large fluctuations and large mismatch between visits and activities A81 Stuttgart - Friedrichshafen: 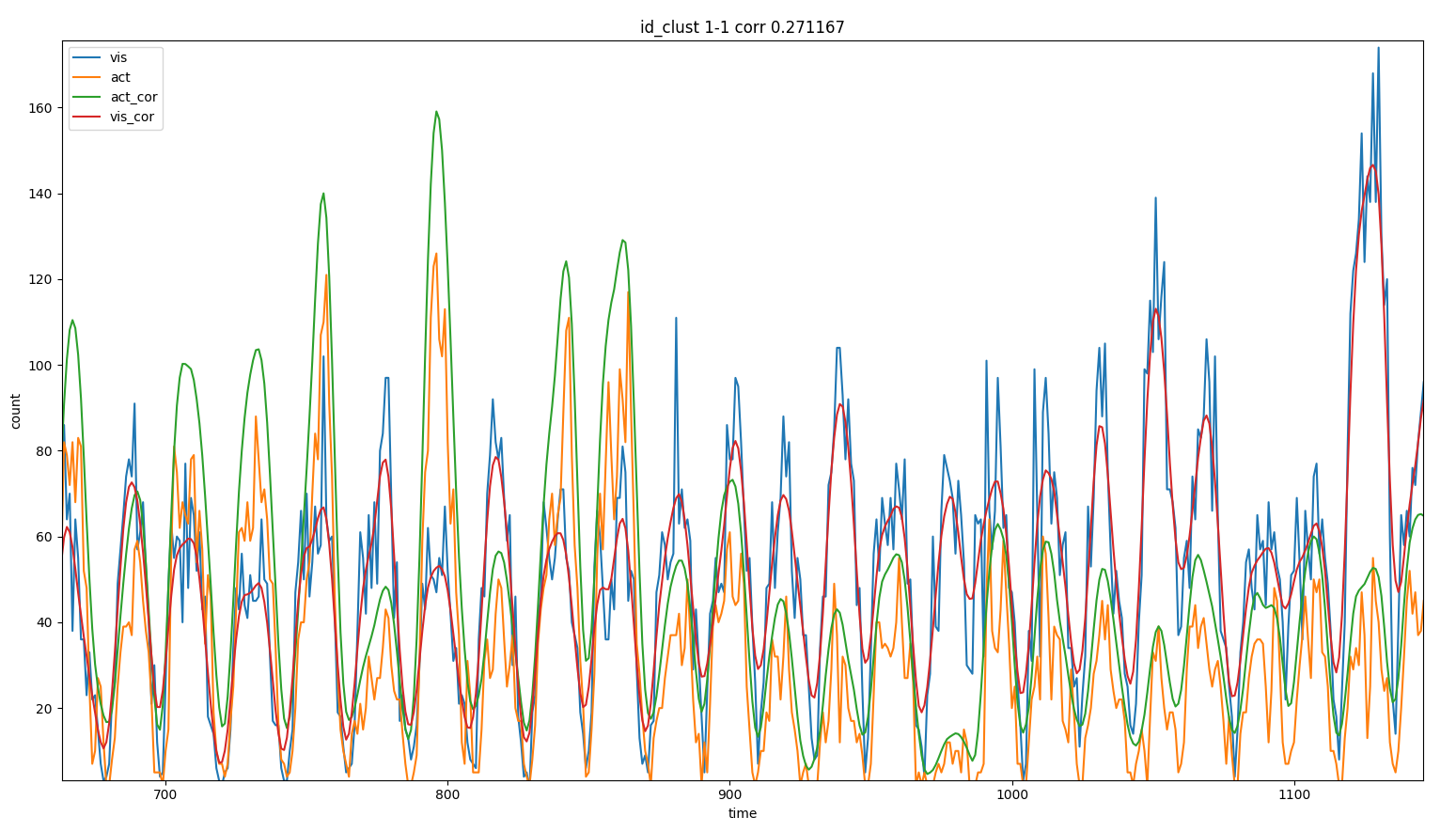for some locations fluctuations are large and activities and visits don’t correlate

Skew VIII - market share

Our user base is mainly composed by business traveller that during week days might represent over 50% of the market share on the motorway during working days. During weekends the number of business traveller is lower represented, especially on sundays.

We see a large discrepancy in the difference between visits and activities depending on week days. 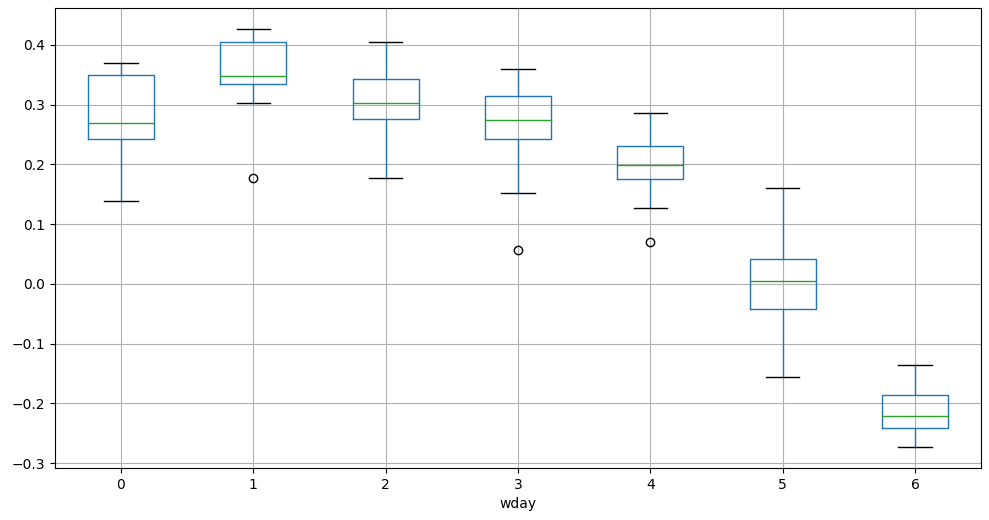boxplot of the difference between visits and activities depending on the week day

Skew IX - weather

Weather has an influence on deviation as well, we can show for example how the minimum temperature influences the mismatch. 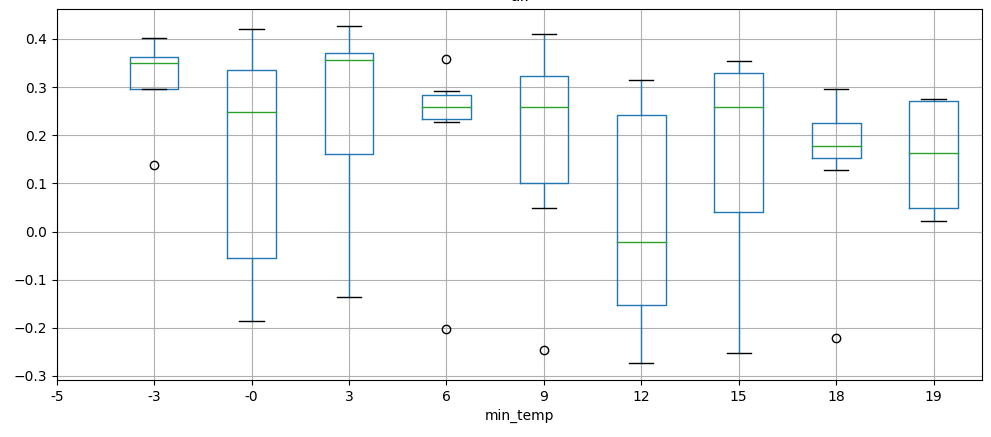deviation vs minimum temperature, binned

We select the most relevant weather features over a selection of 40. 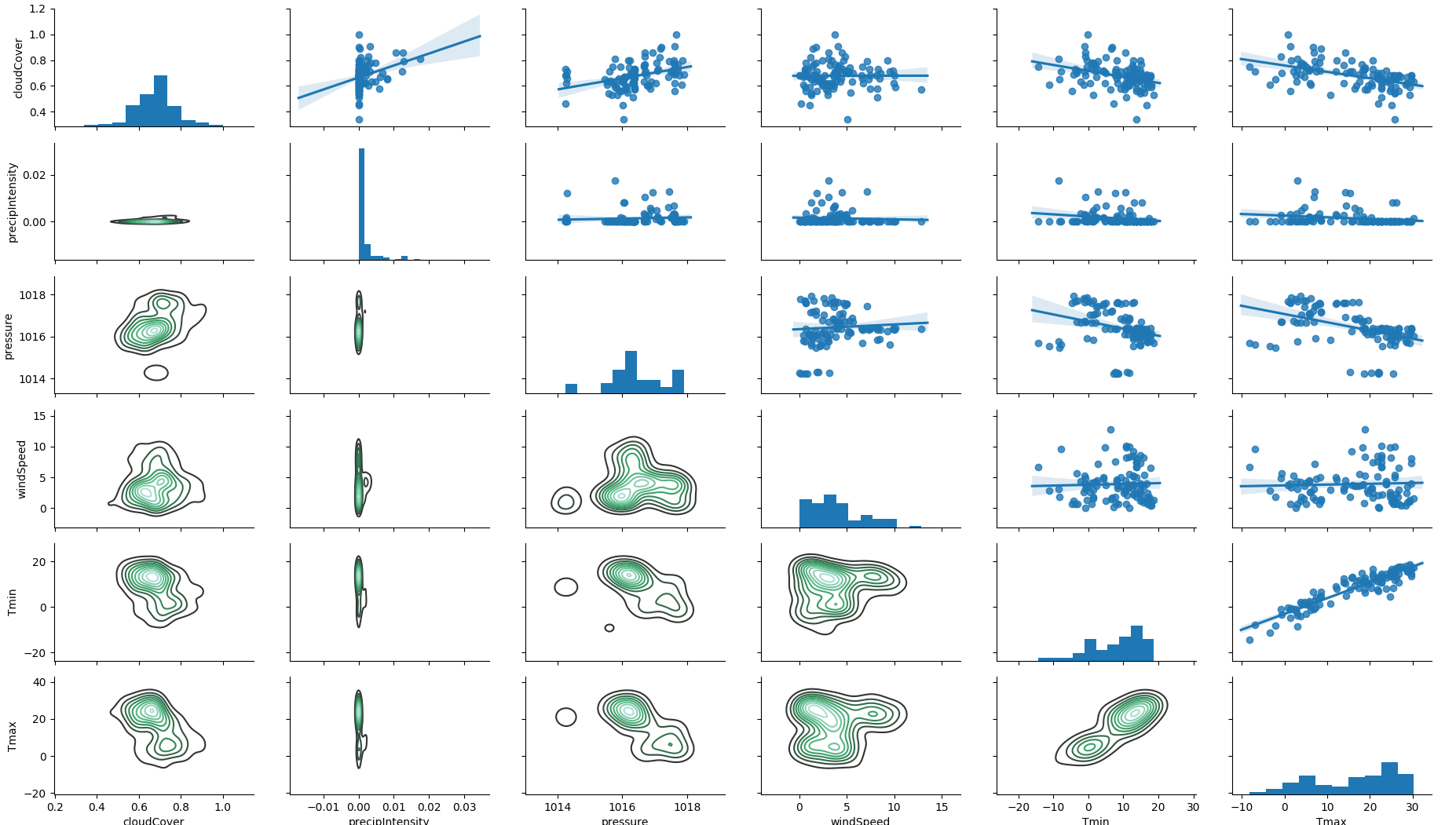correlation between weather features

Other weather related parameters have an influence on the mismatch. 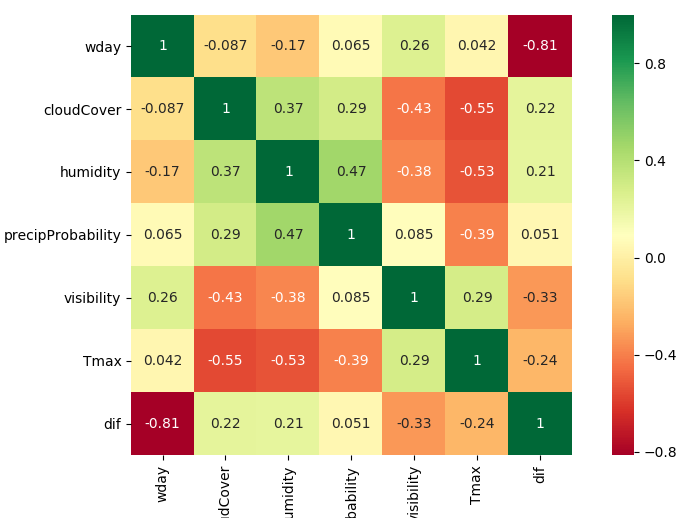weather has an influence on the deviation: di../f/f

We use the enriched data to train a regressor to adjust the counts.

Skew X - commuter vs touristic

Each street has a different pattern concerning the week day. We can simplify the cataloge classifying street segments with the label commuter or touristic. We use the kears library to load and parse bast data.

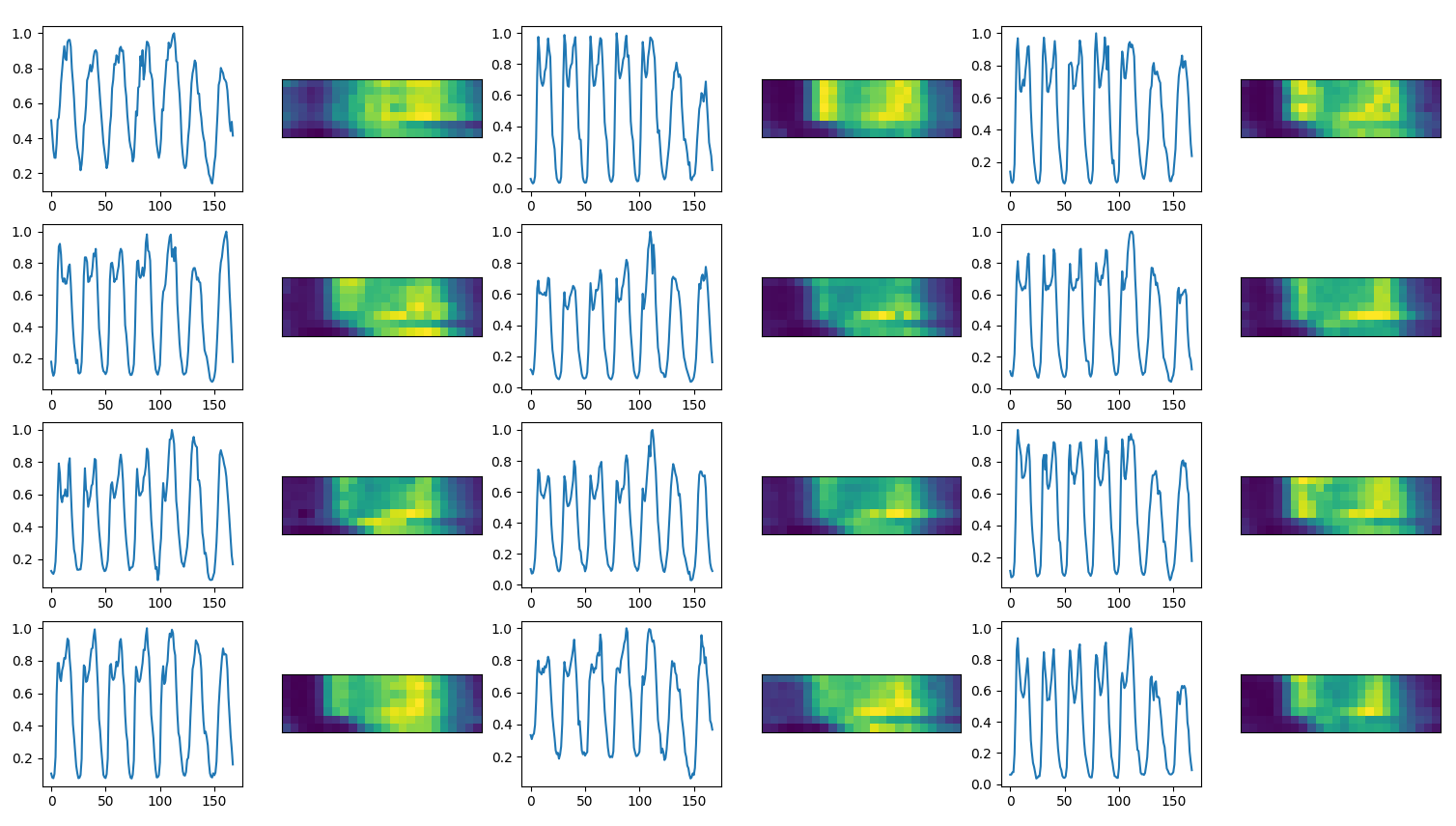BaSt raw data, some locations have a daily double peak, some locations have more traffic on the weekend

We control the performances of an autoencoder on BaSt raw data:

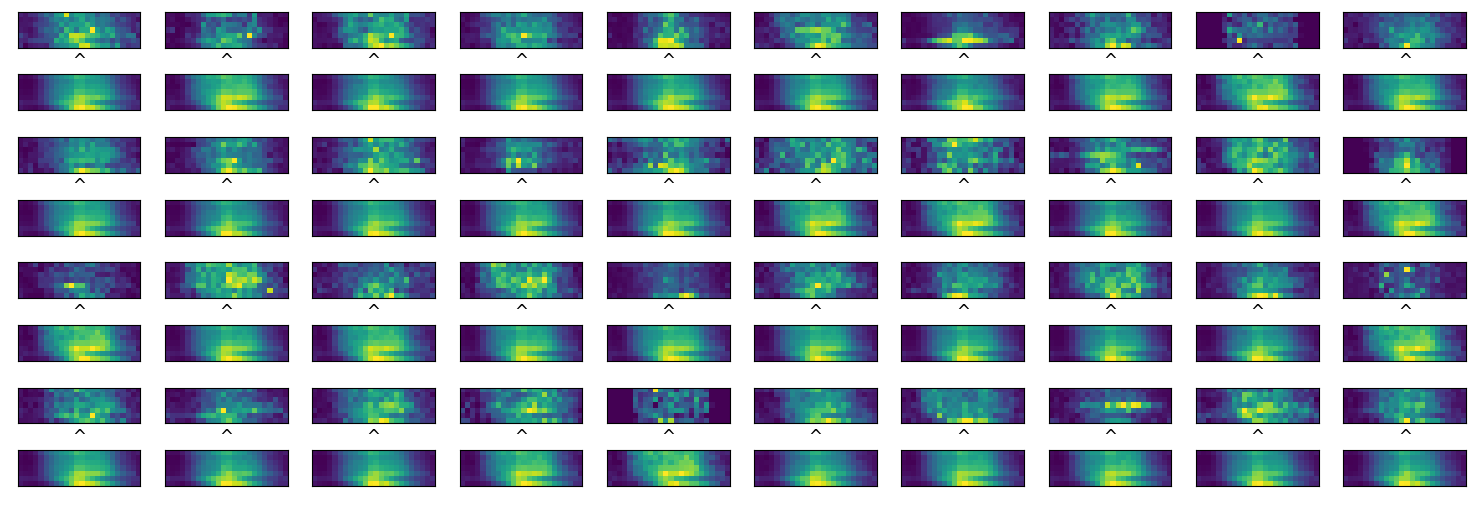Performances of the BaSt autoencoder, fluctuations are flattened

Commuter segments show higher counts during the week, the touristicc over the weekends. Our reference data are the BaSt counts which provide a correction factor for the weekday, especially friday and sunday:

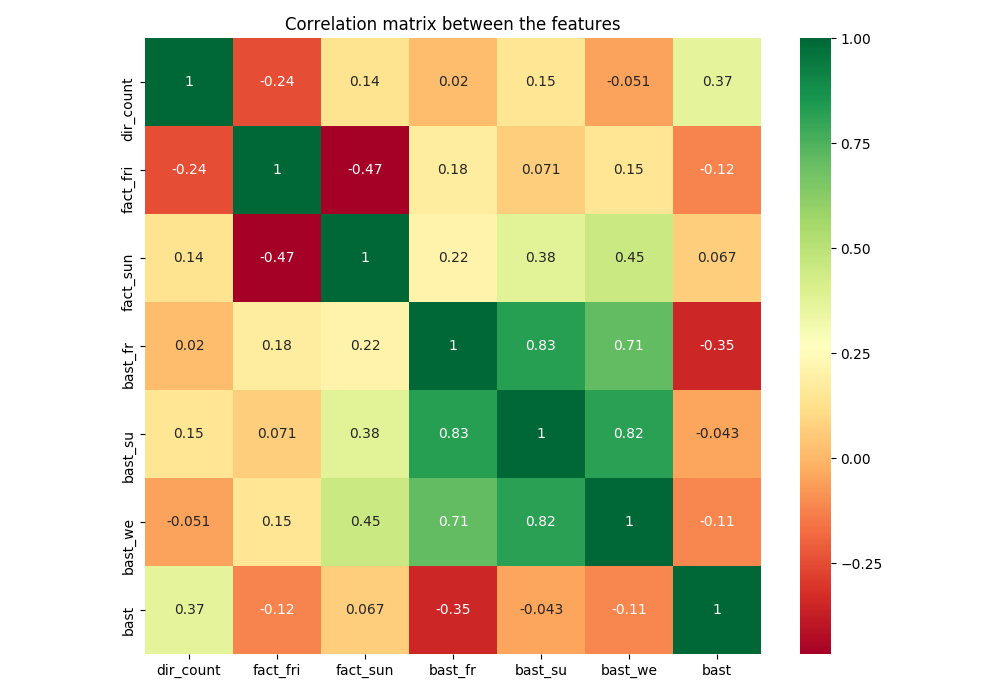correction of direction counts, our numbers counter correlate with reference numbers

We don’t find any significant correlation between BaSt and visits.

Skew XI - population density

Population density has an influnce on mismatch we see bad correlation in dense areas (blue diamond) and good correlation in less populated areas (red diamond

For our training we than consider as well information about population density in an area of 2 km. we enrich our data with information about population density

Skew XII - directions

Sometimes direction distiction does not perform well we have good correlation on one side of the motorway (red diamond) and poor correlation on the other side (blue diamond)

Skew XIII - trip distance filter

Motorway drivers show an elasticity effect: their cell phone is bounded in a cell for a distance longer than a walker. In many cases BSEs do not cover the region of the gas station. We than consider many cells around the gas station: 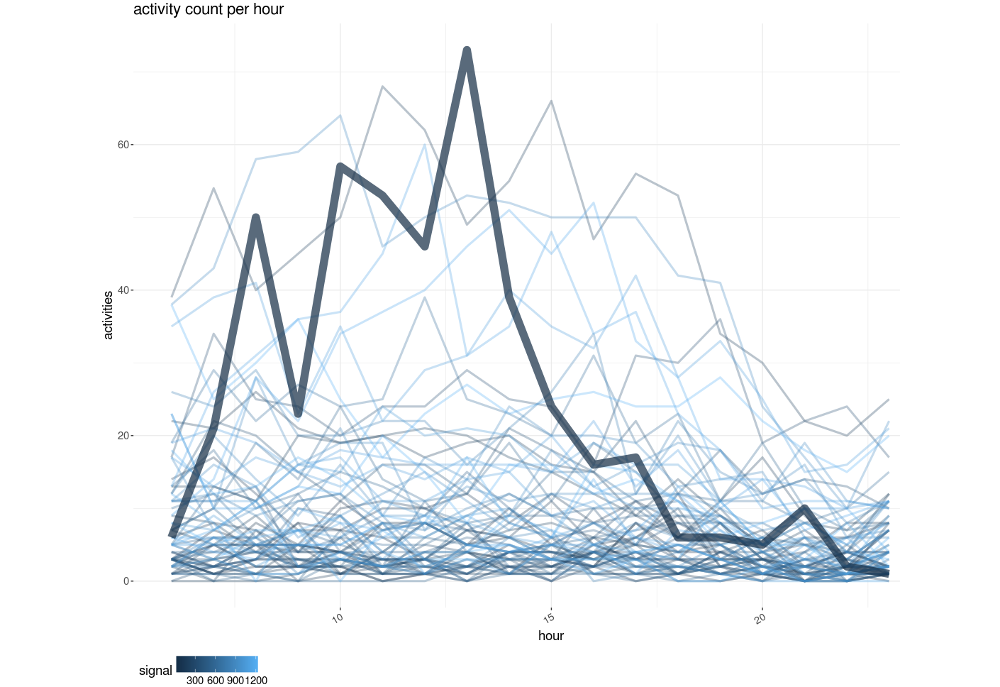example of reference data (thick line) and the activity counts of the cells in its neighborhood

We than apply a trip distance filter to select only users that had traveled a certain amount of km prior to the activity. The filter is optimized on reference data but don’t describe the real activities of motorway drivers. 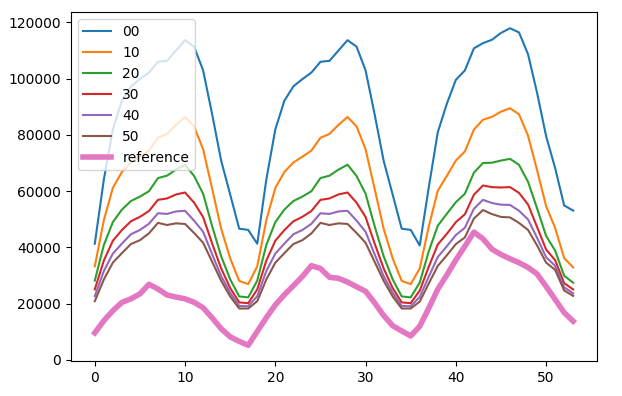trip distance filter optimized on activity counts

Skew XIV - low counts

We see that low counts have an higher relative error.

Locations with few visits per day are the hardest to match, precision depends on absolute numbers.

boxplot of counts deviation relative to number of visitors

Skew XV - device type

Tracks are guests of specific gas stations and carry different devices.

huge parking spot for tracks

Skew XVI - people/car vs people/receipt

The number of people per car changes over weekday. We expect a similar behaviour in the numer of people per receipt.

deviation of the mean number of people per car during a week (red line)

Feature importance

We studied the statistical properties of a time series collecting the most important features to determine data quality. most important statistical properties of time series

We calculate the feature importance on model performances based on statistical properties of time series of reference data. 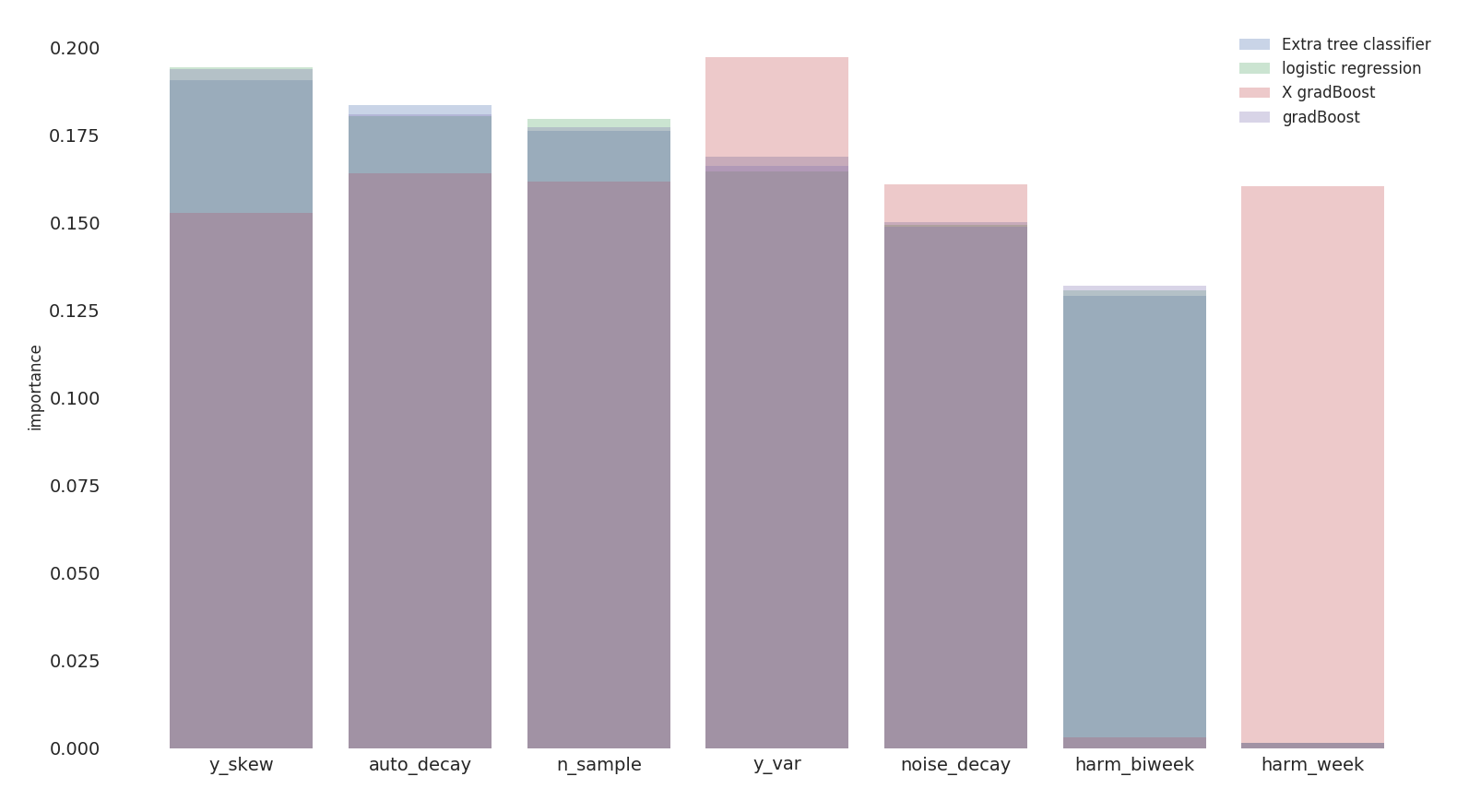we obtain a feature importance ranking based on 4 different classification models

• daily_vis: daily visitors
• auto_decay: exponential decay for autocorrelation –> wie ähnlich sind die Tagen
• noise_decay: exponential decay for the power spectrum –> color of the noise
• harm_week: harmonic of the week –> weekly recurrence
• harm_biweek: harmonic on 14 days –> biweekly recurrence
• y_var: second moment of the distribution
• y_skew: third moment of the distribution –> stationary proof
• chi2: chi square
• n_sample: degrees of freedom

We try to predict model performances based on statistical properties of input data but the accuracy is low which means, as expected, that the quality of input data is not sufficient to explain the inefficiency in the prediction. 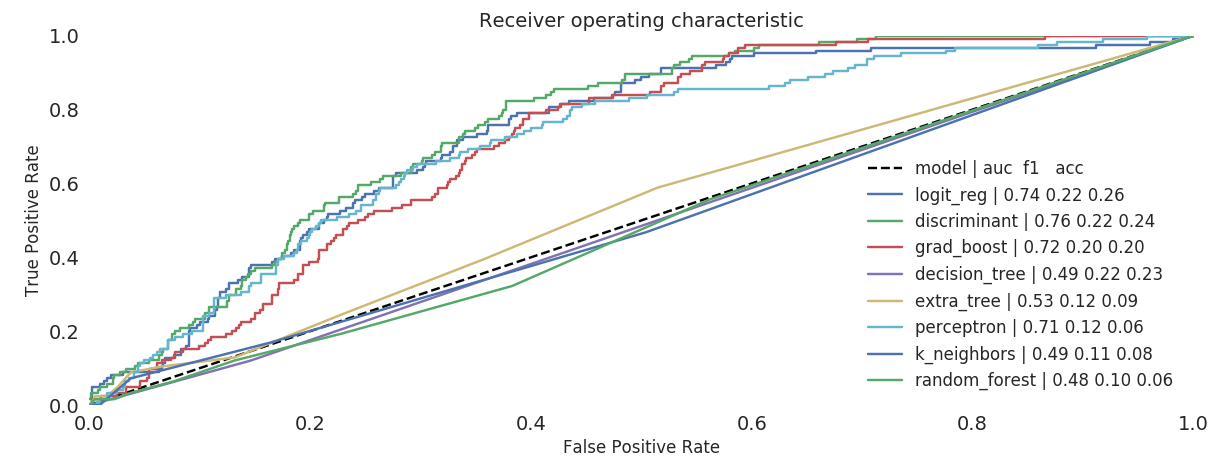training on statistical properties of input data vs model performances

We now extend our prediction based on pure reference data and location information 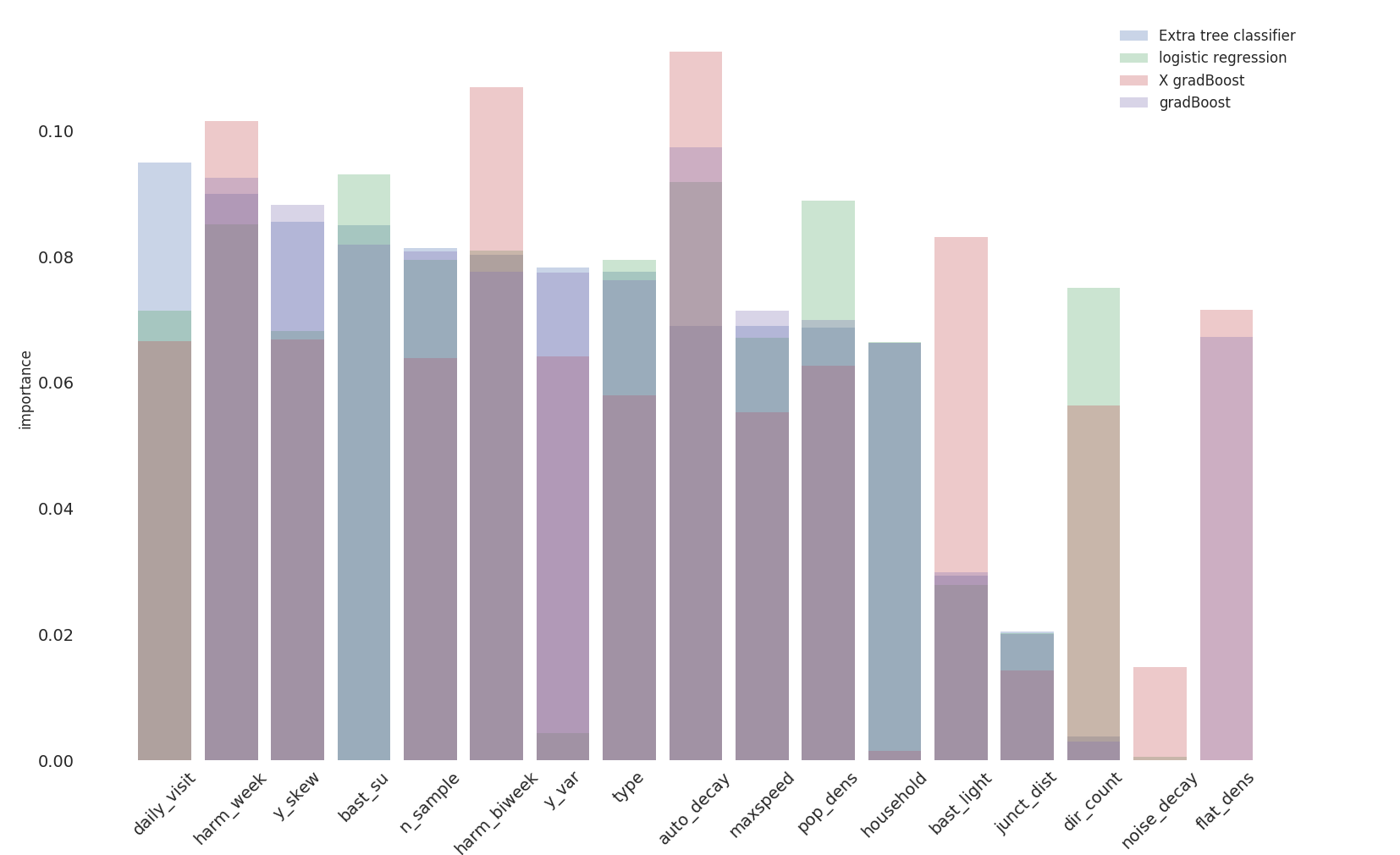feature importance based on location information and input data

Knowing the location information we can predict the performace within 80% of the cases. 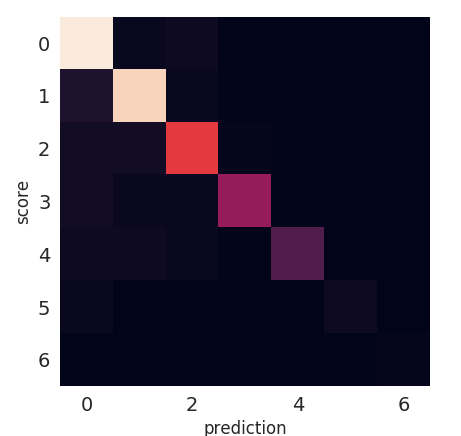confusion matrix on performance prediction based on location information

Regression

All the skews we have shown are used to train predictors and regressors to adjust counts: 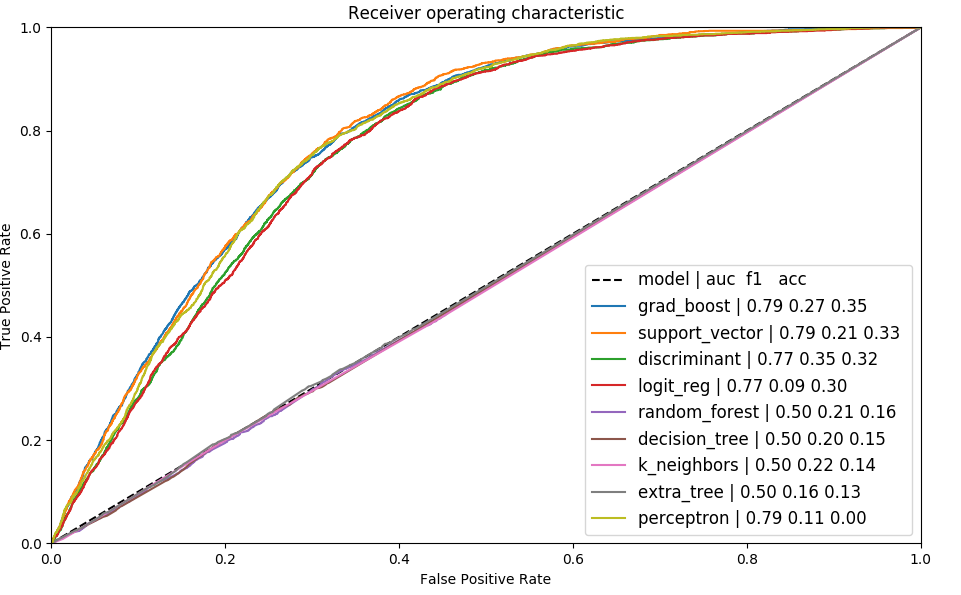ROC of different models on training data

Thanks to the different corrections we can adjust our counts to get closer to reference data. 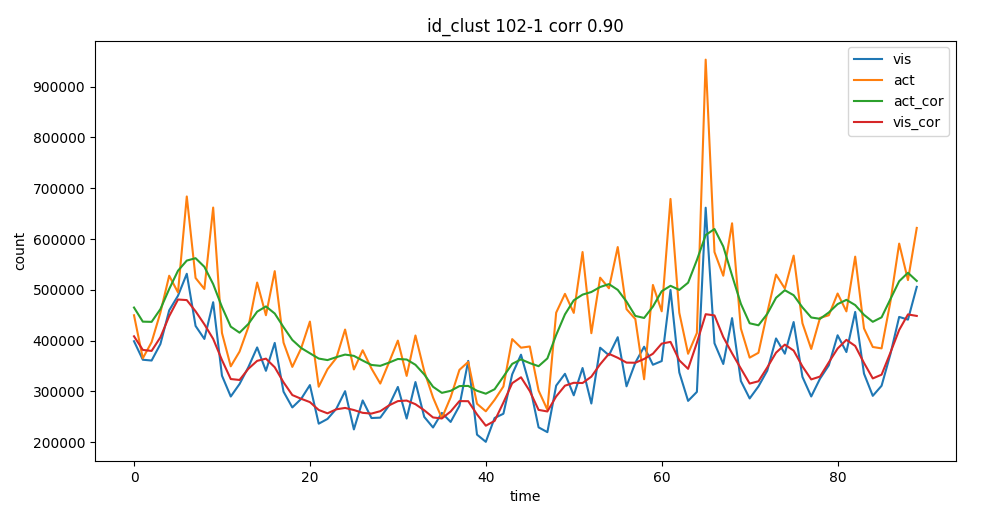corrected activities after regressor

We have structure the analysis in the following way: structure of the calculation for the yearly delivery

We can than adjust most of the counst to meet the project KPIs

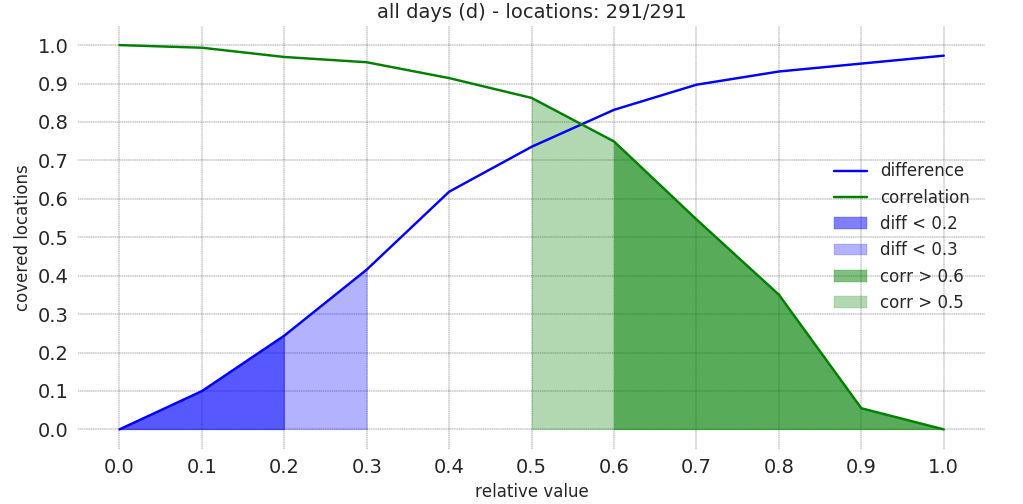distribution of the KPIs ρ and δ

Other reference data

We have scraped from internet other reference data to evaluate the accuracy of our models: i.e. google maps, which consists in normalized time series called popularity.

popularity of a gas station and the css attributes we scrape from internet

Screaping the page we can extract the information about the curves etl_google.js.

var occTime = []
$.each( $('.section-popular-times-graph'), function(i,curveL) {
    $('.section-popular-times-value',curveL).each(function(j,labL) {
    occTime.push(labL.parentNode.attributes['aria-label'].nodeValue);
   });
});
copy(occTime);

A more sofisticated project uses selenium selenium.js to create a bot which searches for a location with the same name of the POI. It selects the more plausible result using Levenshtein distance, waits the page to be loaded and reads the css attributes for the popularity curves and saves them.

We can then overlap the curves and calculate the mutal agreement between sources 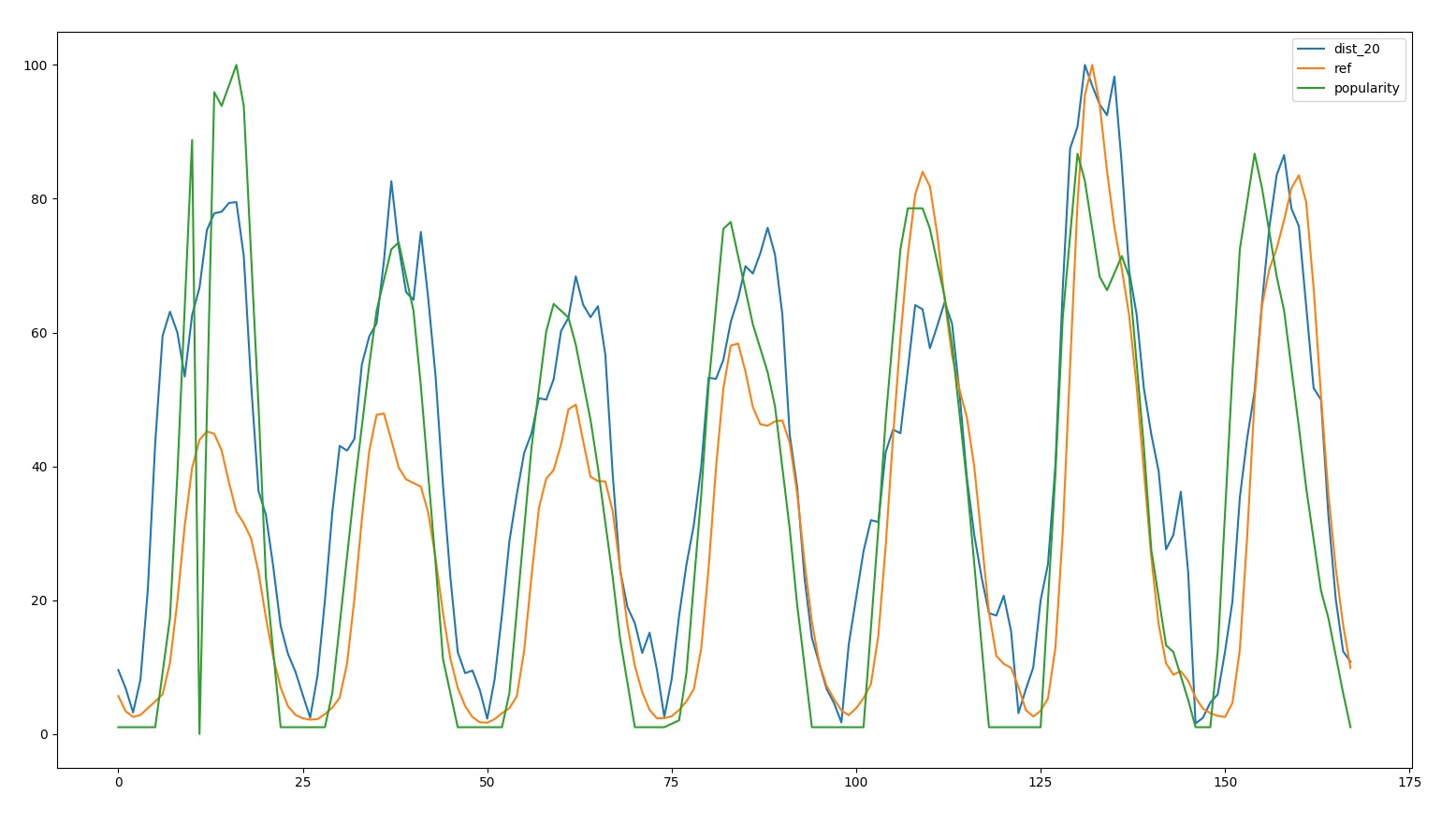activities, visits and popularity for a location

We than see that the agreement between visits and activities is the largest. 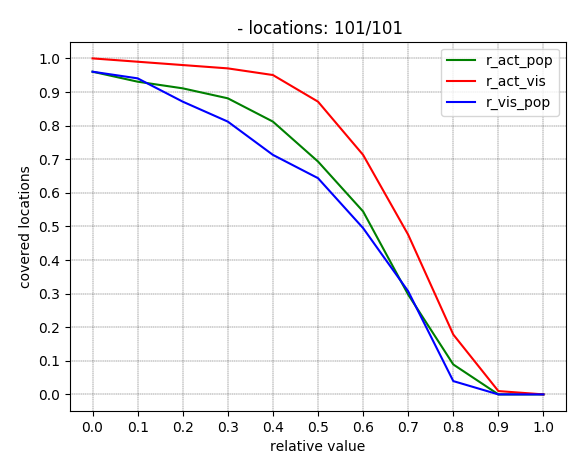accuracy between activities, visits and popularity

Correlation with restaurants

We now see the correlation between a service station and a restaurant.

To build the comparison we build first a pseudo day, ex:

• ‘19-06-08’ : calendar week-weekday-hour

Service station and restaurant share the same location Both activities share the same potential customers

If we look at the correlation between locations on the same platform:

cor_ Pearson correlation, rank_ Spearman correlation, _d daily values, _h hourly values

Althought the hourly values have a good correlation (same daily trend) daily values have an unpredictable result.

Service station and restaurant share the same location 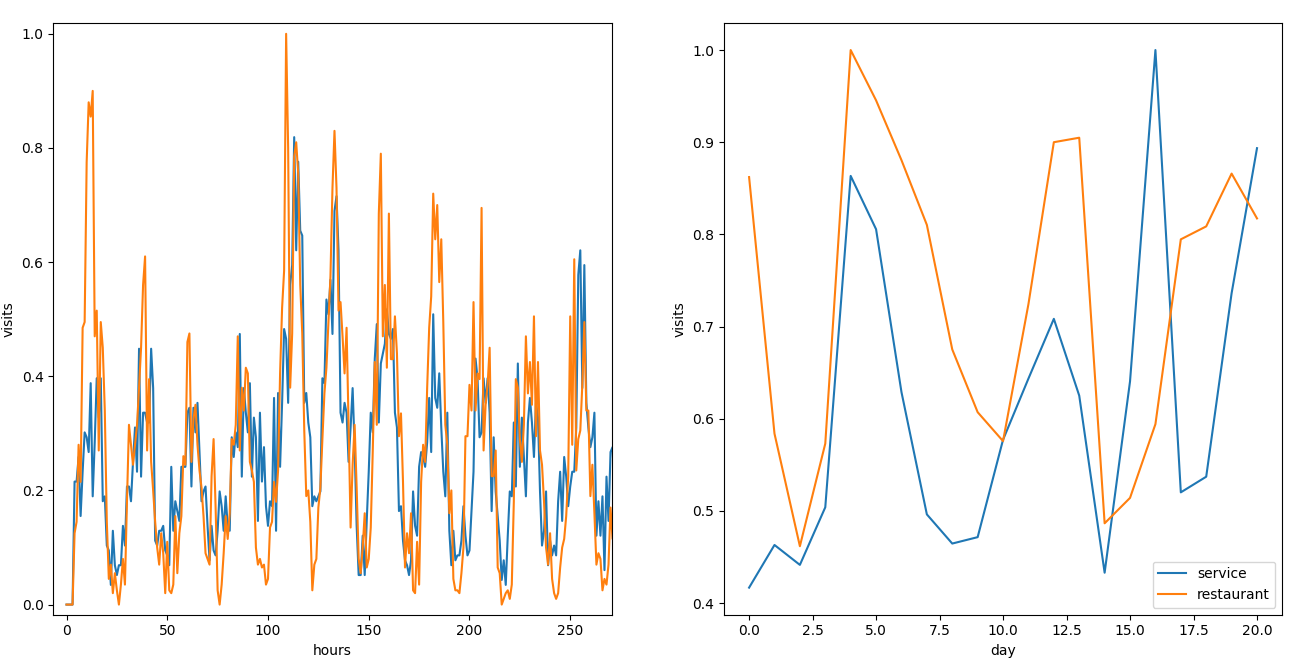difference between the curves, daily values don’t correlate on a pseudo day

If we refer to a real day we have a strong correlation:

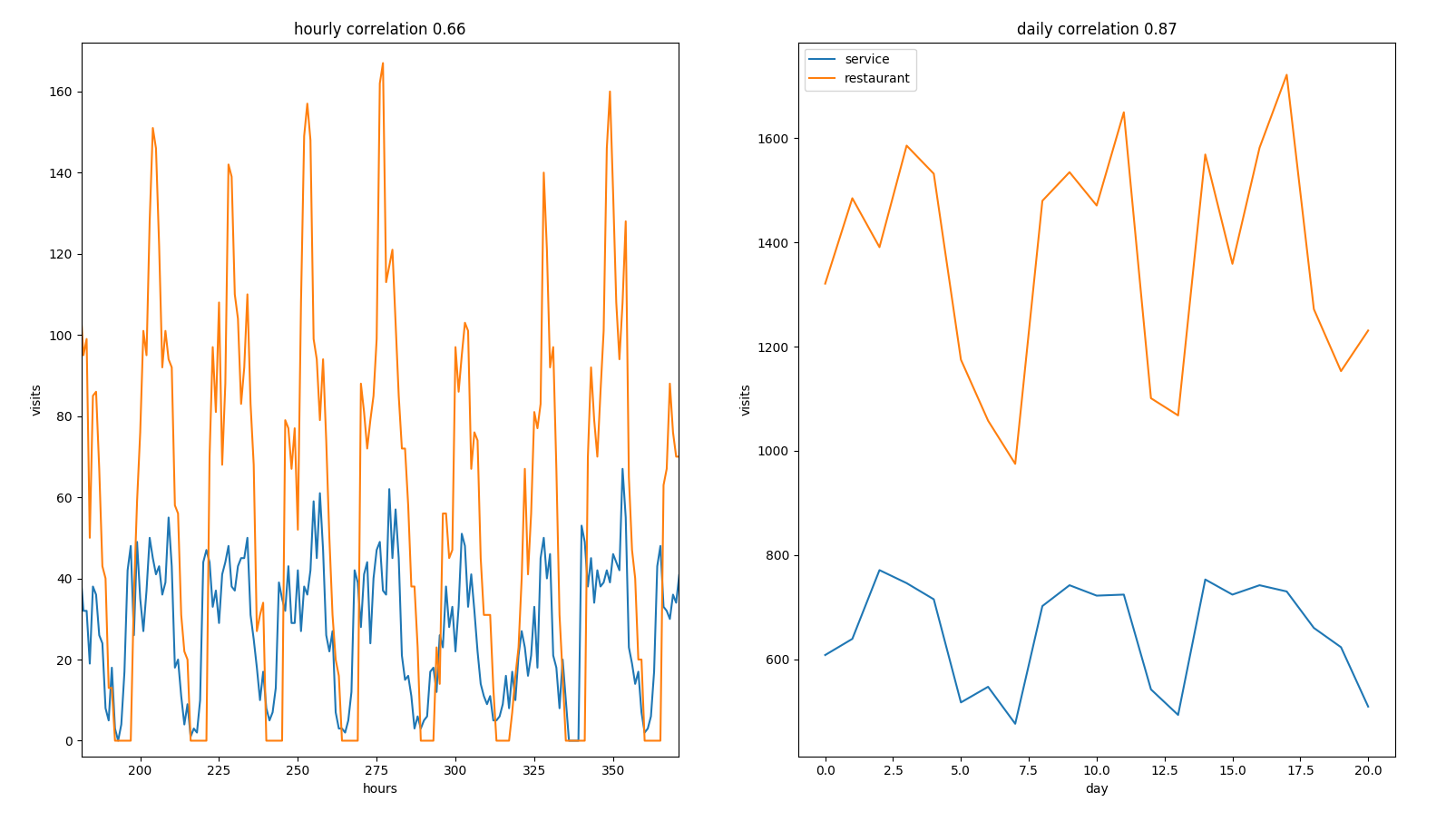correlation between service and restaurant on equal days

That means that we have a bad definition of a pseudo day and we have big fluctuations within days.

Competitor locations

The scope of the project is to count how many motorway drivers stopped by a competitor. The current definition of a competitor is weak since a motorway driver has a more dense options to stop for fuel/eating: customer locations (blue) and competitor ones (purple), a driver has many more options than the ones pointed (from google maps)

It would be much more reliable to label all the users who have been routed on a motorway and report all the activity with a short dwelling time:

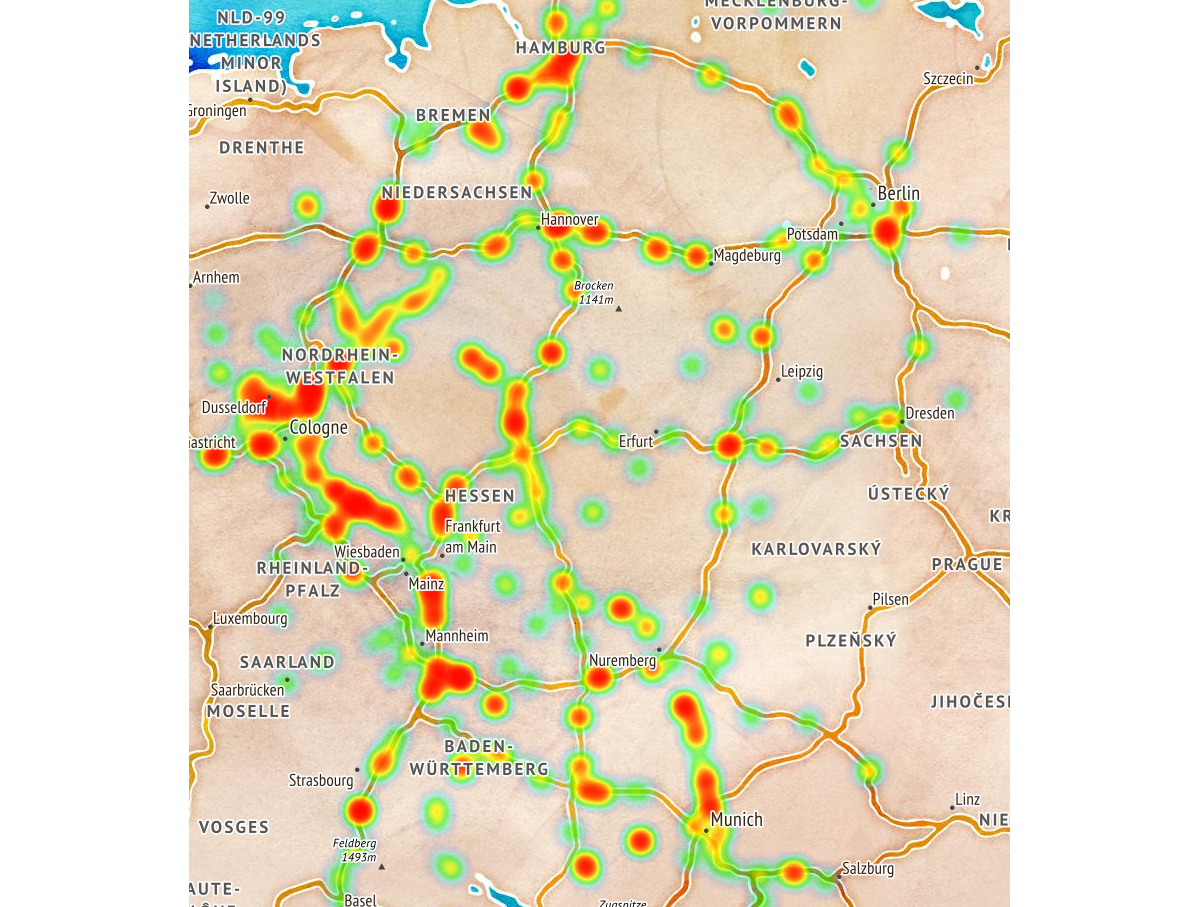heatmap of motorway drivers stopping during a trip

Final remarks

• The mapping between activities and visits need over 15 correction factors to balance all the skews seen in the data.
• Postprocessing corrections seem to be the only realistic way to correct the mismatch.
• The extreme training of the data masks important insights in describing the behaviour of motorway drivers.