generative music composition

A bot that generates melodies and basslines can be uselful for composing. A generative model needs a consistent and clean dataset to learn patters. The output of this project should be a tiny model that could fit on an embedded device to generate midi.

dataset

To train such a bot I start with a collection of songs from my repository https://viudi.it/article/music_composition.html where I parse 21 midi files I written using lilypond markup language

\version "2.12.3"
\include "italiano.ly"
title = "Flut"
date="01-08-2012"
serial ="2"
\include "Header.ly"
melodia = {
  <<
    \transpose do do'
    {
       r2 r8 re mib sol |
       re8 sol la sib do' sib la sol|
       re8 sol  la sib  do' sib  la4|
    }
armoniaIII = {
  \chordmode {
  mib1 do:m re:m sol:m
  sib1 la:m re':m sol:m
  }
}

Which creates midi files and tidy music notation

flutto_note partiture generated by lilypond

Unfortunately I couldn’t find a suitable lilypond lbrary in python so I had to parse the midi generated by lilypond and recreate a lilypond style of music notation. Songs are usually made out of an harmony (piano) lead (violin) and bassline (cello-bass).

flutto_note data used for training

tokenizer

We need to decide how we tokenize the data and we decide for an explicit notation instead of the compact one:

chord notes
C do-mi-sol
D4/sus4/addb3 re-fa-sol-la

Which is often not really compact

flutto_note complicated chord notation

We explicitely write down the chord although we know chords with the same notes written in different notations they have different meaning. To ease the learning process we always display the chord in ascending order.

def order_chord(chordL,stem_octave=False):
    if stem_octave:
        replace = {",,":"",",":"","'":"","''":""}
        rem_octave = re.compile("(%s)" % "|".join(map(re.escape, replace.keys())))
        chordL = [rem_octave.sub(lambda mo: replace[mo.group()],x) for x in chordL]
    try:
        pL = [NOTES.index(x) for x in chordL]
    except:
        pL = list(range(len(chordL)))
    return np.argsort(pL)

Music has far less tokens than languages but notes have more attributes than words and structures are somehow more essential than grammar: a note by itself it doesn’t mean anything without rhythm, scale and timbre while languages can be really grammatically simple.

That poses many questions on how to embed music, ideally for each note we can create different layers of embeddings:

and for chords:

but we can alternatively increase the number of token and bake all attributes into the token and let the model figure out the relationships.

Whatever the strategy is we need to decide for an encoding and vectorization of the layers. We start from a language like representation dividing the data set bar by bar.

('do-mi-sol', "[start] mi'16 do'16 la16 si16 do'16 la16 si16 do'16 re'16 si16 do'16 la16 sol16 si16 do'16 si16 [end]")
('fa-la-re', '[start] re8 mi8 fa8 re8 mi8 fa8 sol8 mi8 [end]')
('fa-re-sib', '[start] la8 sib8 la8 sol8 fa8 mi4 fa8 [end]')
('re-si-sol', '[start] sol16 fad16 sol8 fad16 mi16 fad16 sol16 la16 si16 la16 sol16 fad8 sol0 [end]')
('do-mi-sol', '[start] re8 mi8 fa8 sol4 mi4 fa8 [end]')

same for the bassline.

We then go for a 100 tokens vocabulary size (notes are 128 but much less are used, chords are 12 notes times few modes and after deduplication probably 60-70). If we would use more attributes tokens would be 12 for notes, 4-5 for octaves, 4-5 for modes.

    n = ['do','dod','re','mib','mi','fa','fad','sol','lab','la','sib','si']
    c = {"M":[0,4,7],"m":[0,3,7],"sus":[0,5,7],"dim":[0,3,6],"m7":[0,3,7,9]}

We write a routine like:

def iterate_chords():
    l = ['C','C#','D','D#','E','F','F#','G','G#','A','A#','B']
    n = ['do','dod','re','mib','mi','fa','fad','sol','lab','la','sib','si']
    n2 = n + n + n
    c = {"M":[0,4,7],"m":[0,3,7],"sus":[0,5,7],"dim":[0,4,6],"m7":[0,3,7,9]}
    m = list(c.keys())
    s = {}
    for i, l1 in enumerate(l):
        for m1 in m:
            k = l1 + m1
            l2 = l.index(l1)
            c1 = "-".join([n2[x + l2] for x in c[m1]])
            s[k] = c1
    return s, s1

and we get a list of unique 60 chords:

'C:M': 'do-mi-sol', 'C:m': 'do-mib-sol', 'C:sus': 'do-fa-sol', 'C:dim': 'do-mi-fad', 'C:m7': 'do-mib-sol-la', 'C#:M': 'dod-fa-lab',...}

We do the same with chords in a scale:

{'C:I': 'do-mi-sol', 'C:II': 're-fa-la', 'C:III': 'mi-sol-si', 'C:IV': 'do-fa-la', 'C:V': 're-sol-si', 'C:VI': 'do-mi-la', 'C:VII': 're-fa-si', 'C#:I': 'dod-fa-lab', 'C#:II': 'mib-fad-sib', 'C#:III': 'fa-lab-do', 'C#:IV': 'dod-fad-sib', 'C#:V': 'mib-lab-do',...}

We see that the deduplicated number of chords per scale reduces from 84 to 60.

We have collected 500+ chords with correspective melodies.

model

results

Within 100 epochs and few minutes of training the loss is 0.1 and accuracy 0.95

We create a series of chords in a given probability. We refer to this work for obtaining a series of Markov chains (depending on authors) around chord progression.

We randomly select a starting chord according to the probability of that author and we proceed with the next chord in the same scale for the probability given by the chain

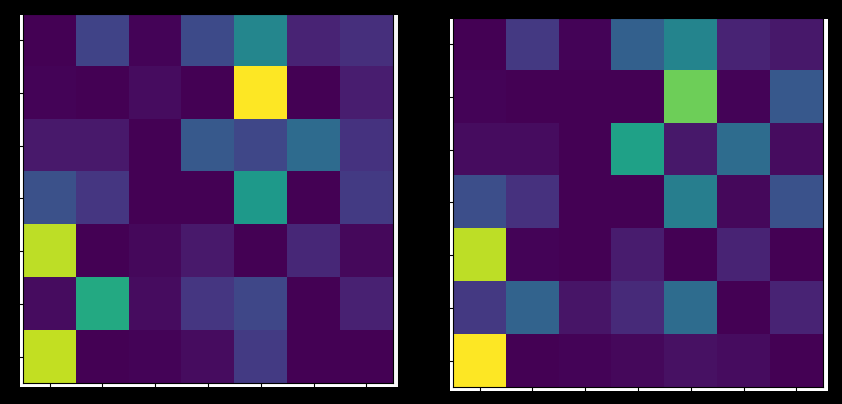markov_bach Markov chains for Bach in major and minor

We selected here G/E:m

['la-re-fad', 'la-do-mi', 'la-do-fad', 'la-do-mi', 'sol-si-re', 'la-re-fad', 'sol-do-mi', 'sol-do-mi', 'la-re-fad',...]

The first results are sadly overfitted

<<mi1 si sol>>  -> sol16 mi16 si16 do16 mi16 re16 do16 si16 do16 si16 la16 sol8 mi8 la16 
<<fad1 la re>>  -> sol16 mi16 si16 do16 mi16 re16 do16 si16 do16 si16 la16 sol8 mi8 la16 
<<re1 si sol>>  -> sol16 mi16 si16 do16 mi16 re16 do16 si16 do16 si16 la16 sol8 mi8 la16

We need to strongly reduce the model parameters (even bacause of long prediction time) from the first model set for language models. We use a minimal set

       ,"vocab_size":100,"sequence_length":20,"batch_size":64
       ,"embed_dim":6,"latent_dim":6,"num_heads":8

and we see that the music turns more interesting

generated music First iteraction of generated music

And here is the example file with some interesting ideas but falling in a loop sometimes and missing the key