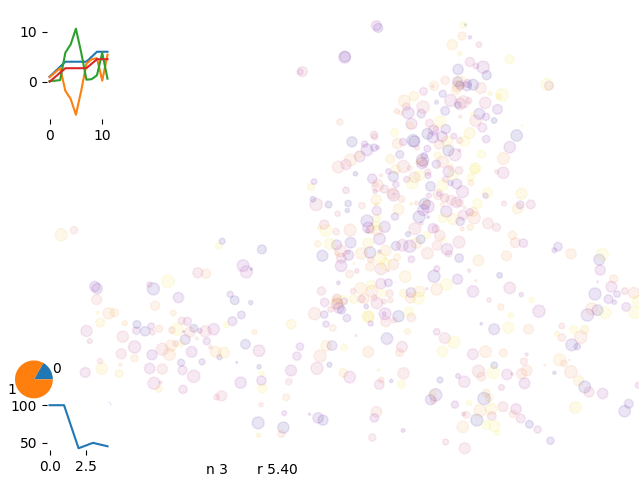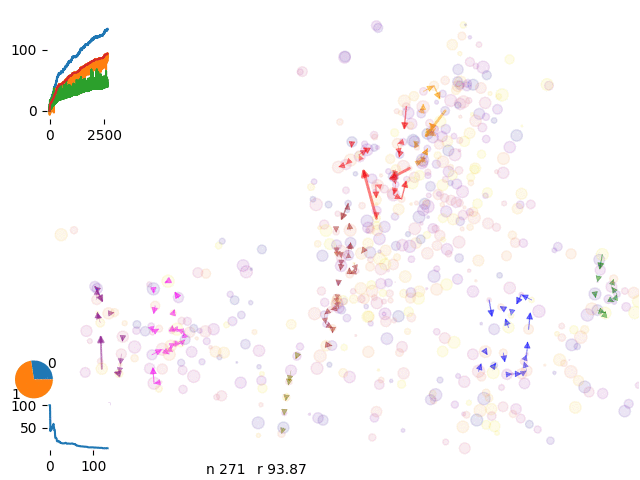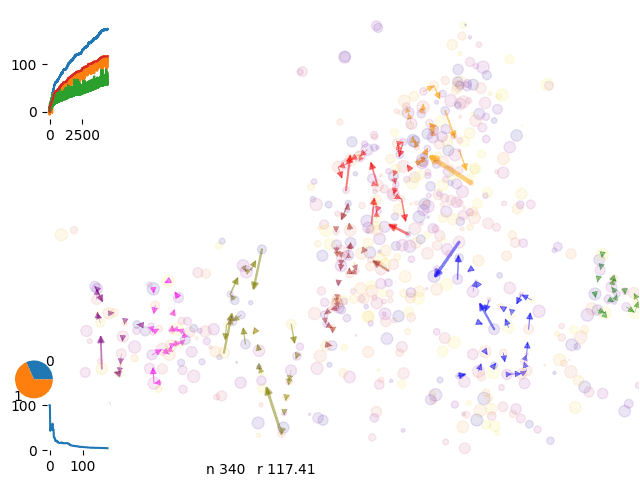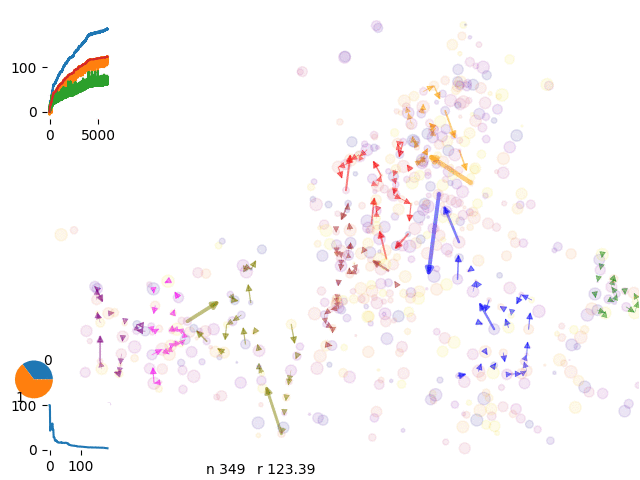Optimization

Optimization is finding one optimal configuration for a given system

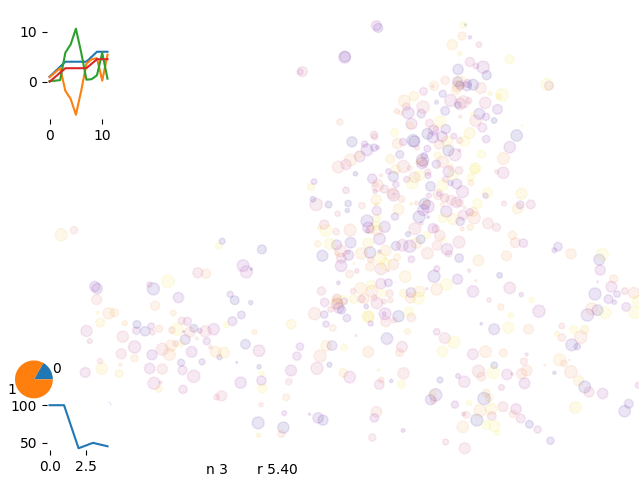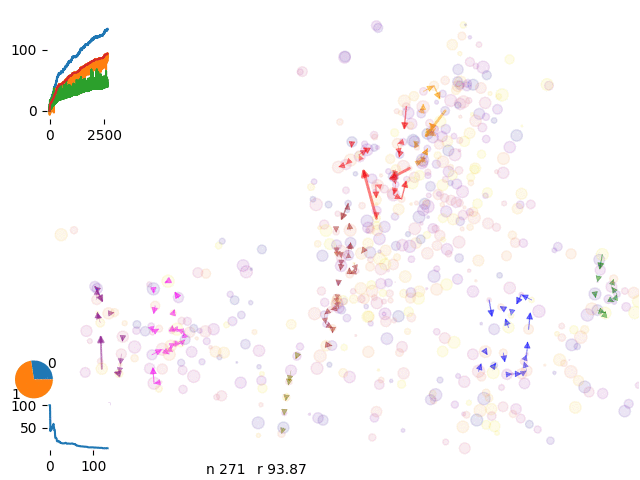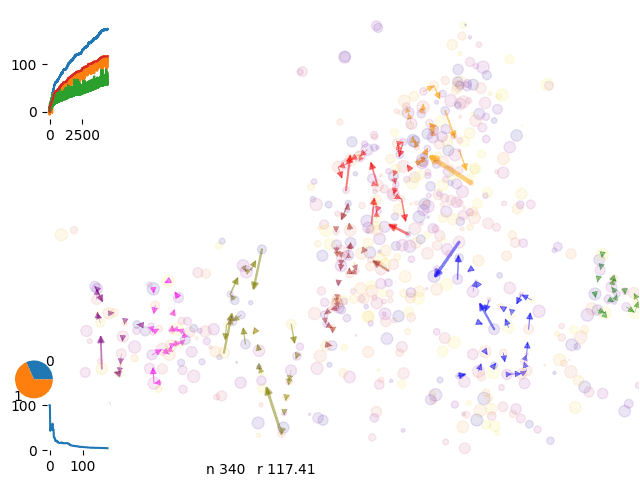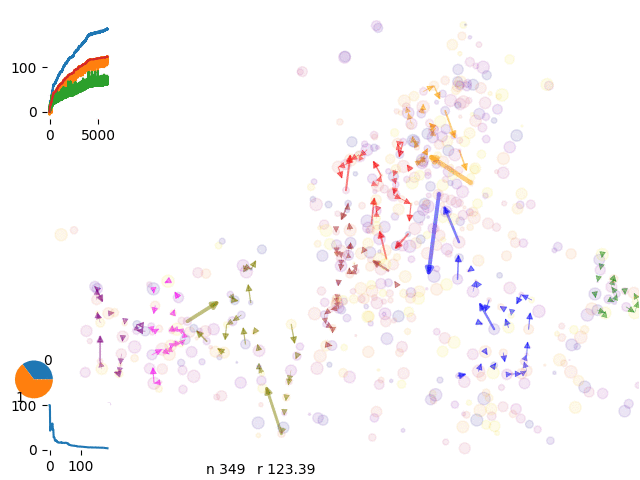optimization 8 vans

optimization task

We have to find the most efficient distribution tasks among drivers to minimize costs and maximize revenue

optimization problem

optmimization engine

We need to reduce the drive time and focus on most interesting spots

routing efficiency

We first add all the spots a van could see and we calculate the most optimal route connecting the spots

spot connection

spot prioritization

Prediction should define the layers where we are most confident about the revenues for a given time and weather condition

We define the revenue as:

potential of that area for a given weekday and shift number

μ_deployn_deployE_deploy + μ_collectn_collectE_collect

Where μ is the potential to add or remove a scooter at a certain spot, E is the revenue per scooter, n is the number of scooters

and the costs as:

l_ridec_lenght + n_stopsc_stops

Where l is the lenght, n the number of stops and c empirical parameters.

The energy calculation considers the single paths and the interaction among them:

mallink_energy

class structure

We display the interdepency

module_mallink

solve problem

We can toggle the activation of the spot and recalculate the energy and apply the Metropolis algorithm to see whether the move is convenient

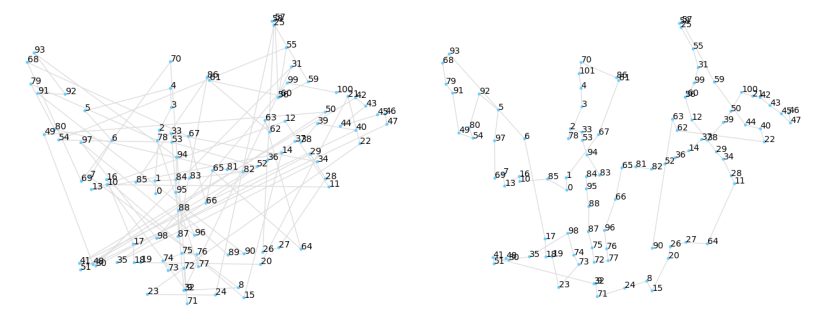
optimization graph

The total energy of the system decreses

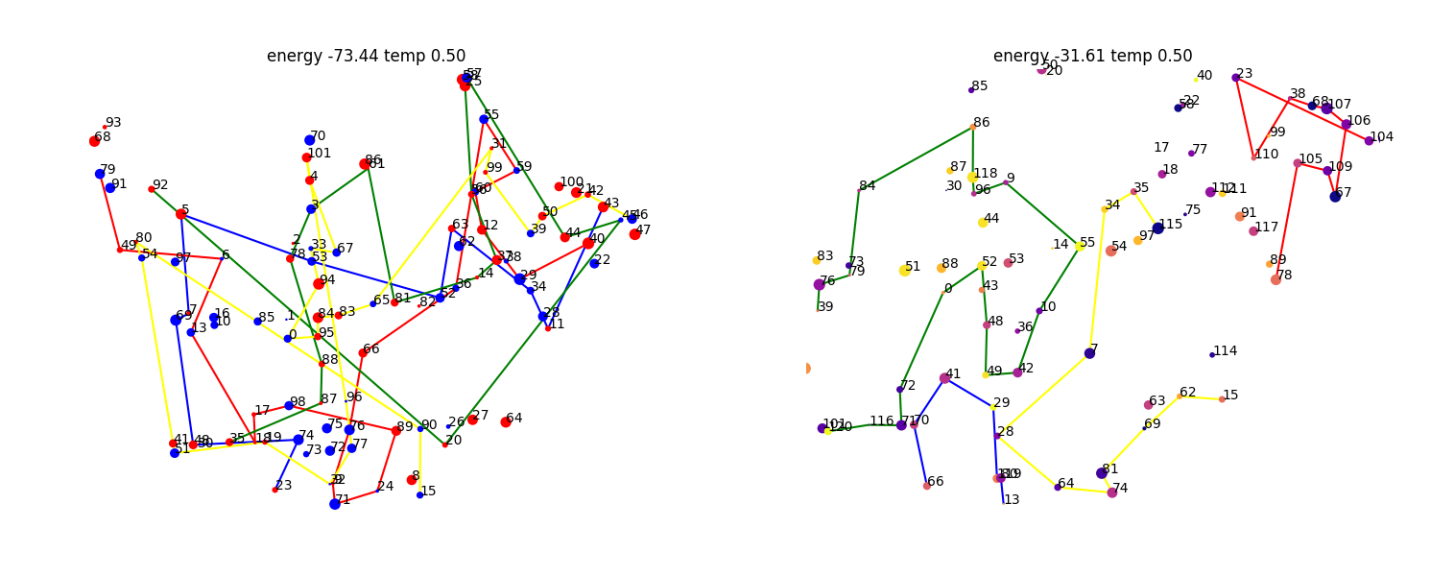
optimization energy

We consider a larger system

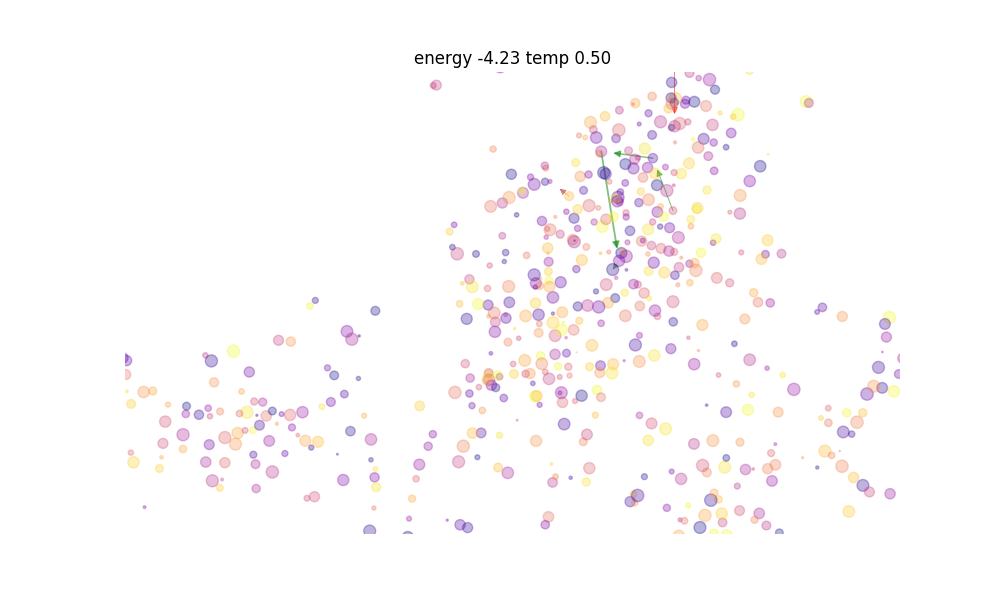
larger system

But after many iteration steps the solution is slowly approaching

optimization energy, slowly learning

Markov chain

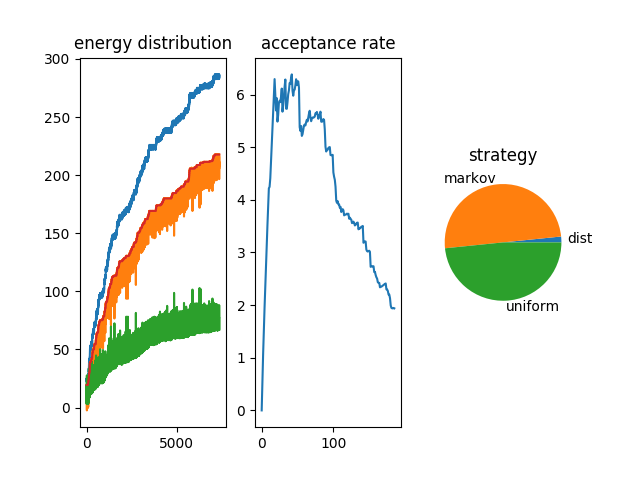
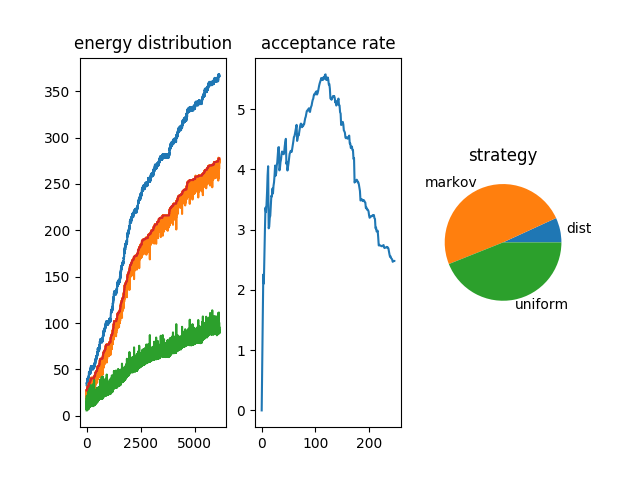
To improve the acceptance rate of moves we introduce Markov Chains

Markov schema

We multiply the Markov chain matrix with itself to condense iteration probabilities and set up a threshold to consider only the most important links

We calcualte at first a really dense Markov chain (first power) and we increase the power (until five) to have a sparse Markov chain

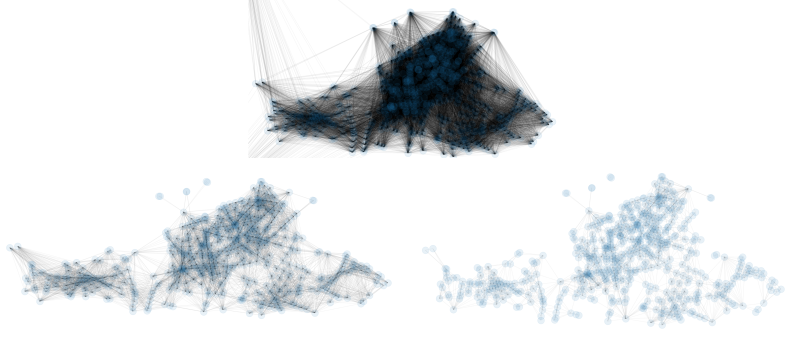
Markov chain densities

We than use a sparse Markov chain with around 7 links per node

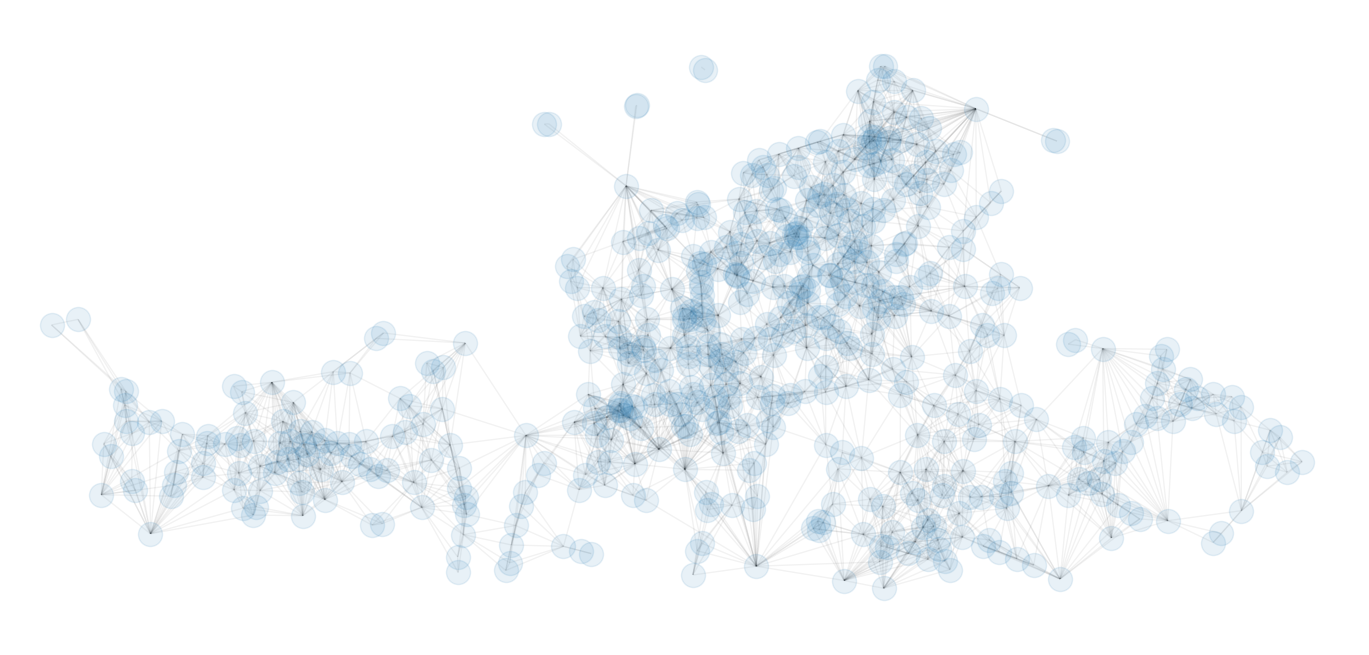
sparse markov chain

From the Markov chain we create a cumulative probability which is getting simpler while increasing the number of iterations

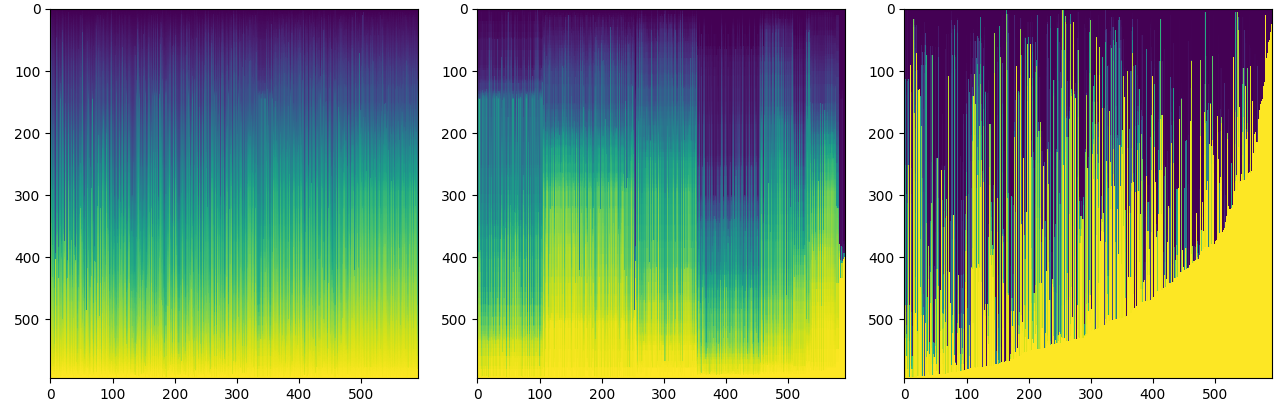
cumulative probability on filtering

iterating to the solution

We run over 500 spots and 8 drivers

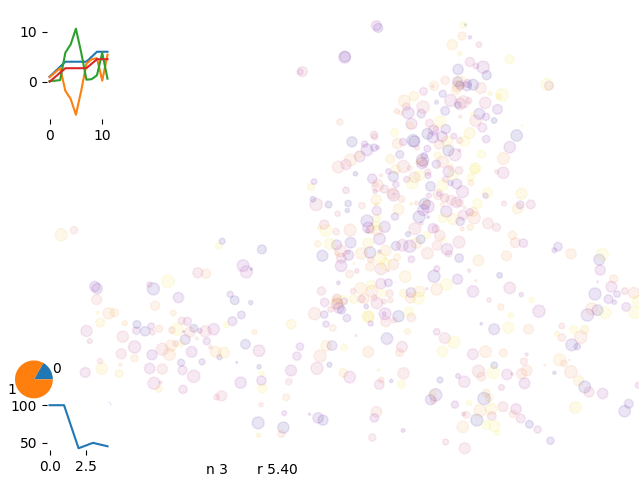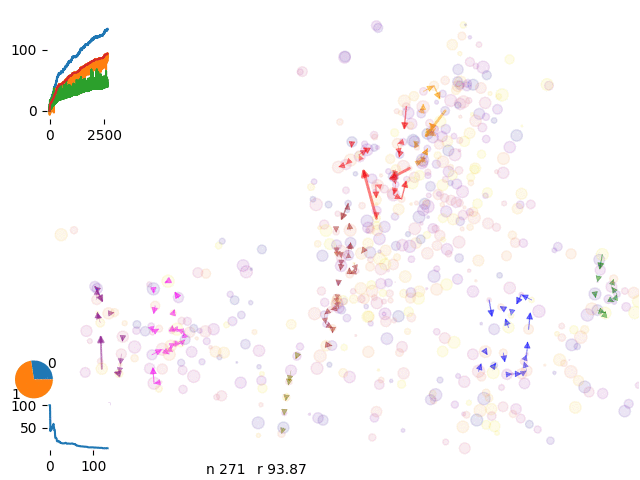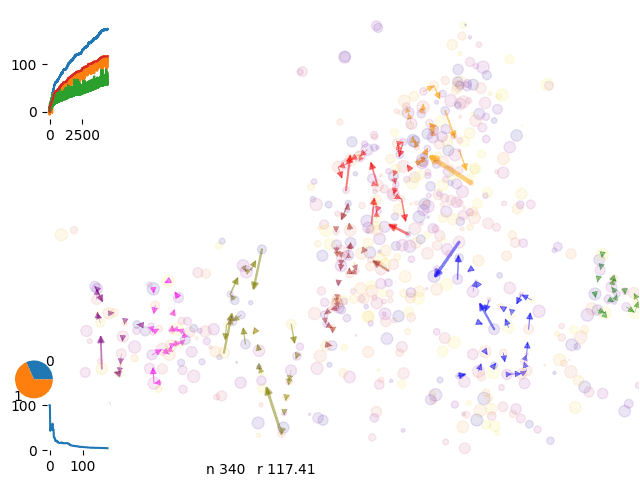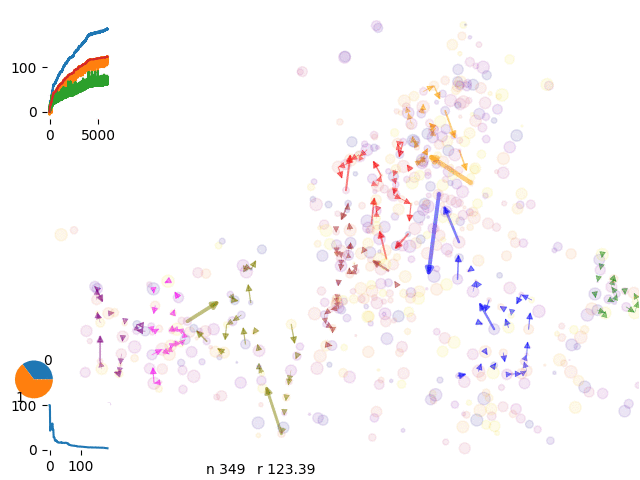optimization 8 vans

and iterate over different solutions

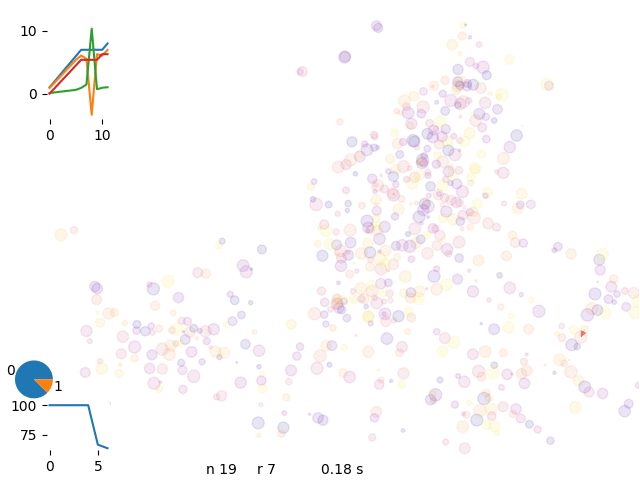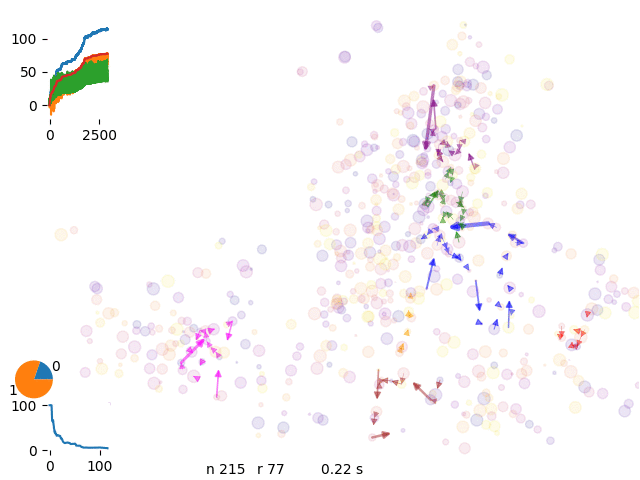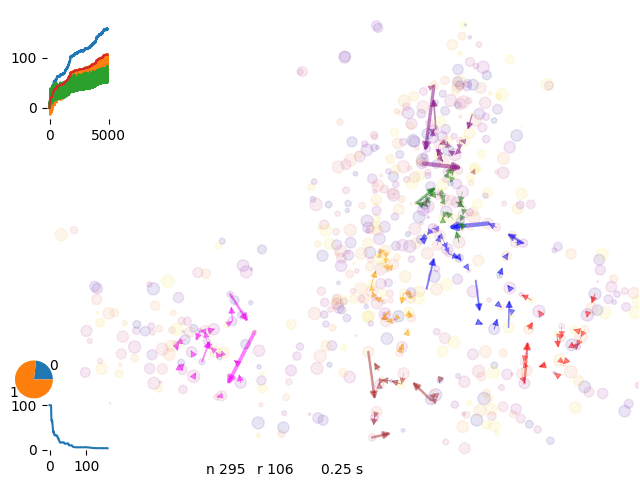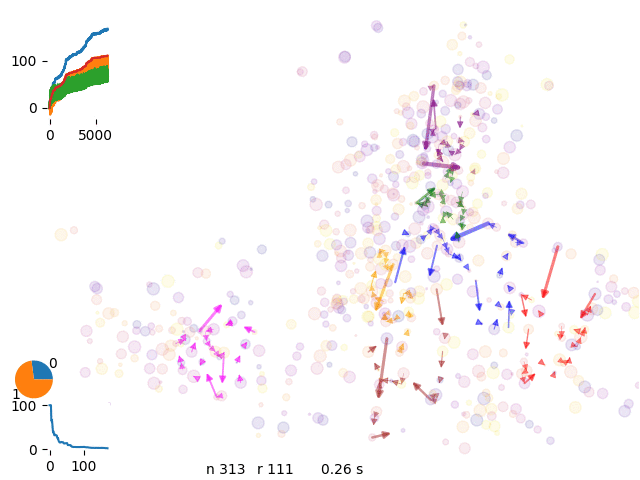
optimization 8 vans

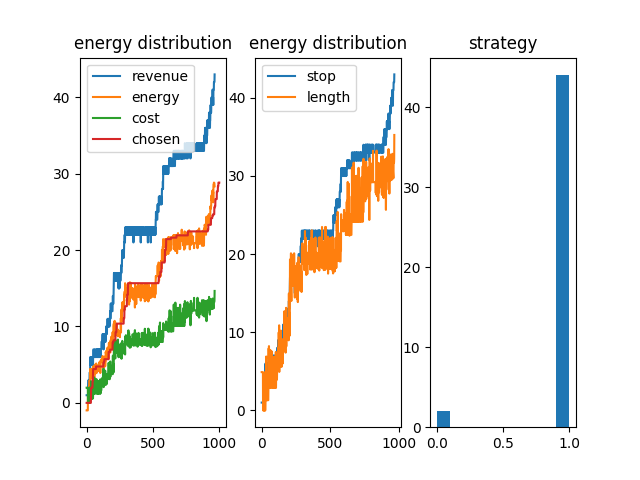
We can control the energy evolution and check the aymptotic behaviour of the curves.

energy history with 8 vans

single task move

The engine was at first focusing on single task move which was making convergency pretty slow. We started than introducing new moves and initial set up

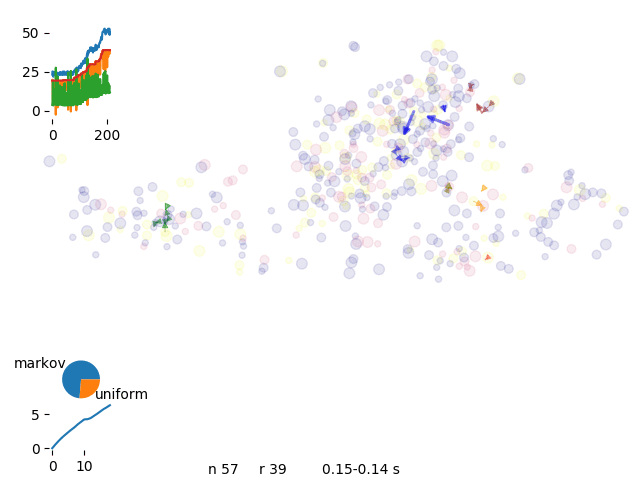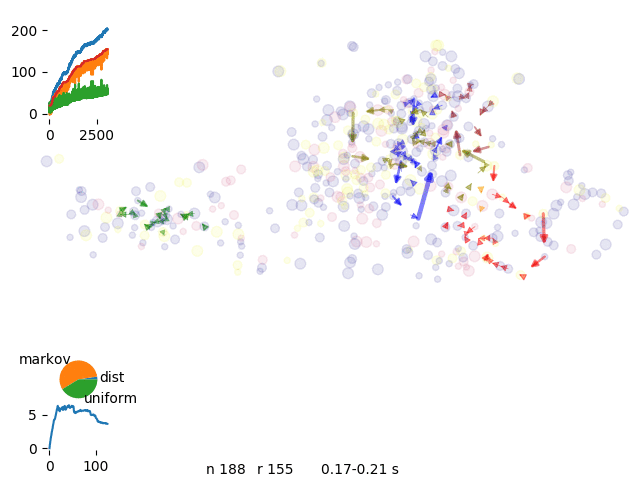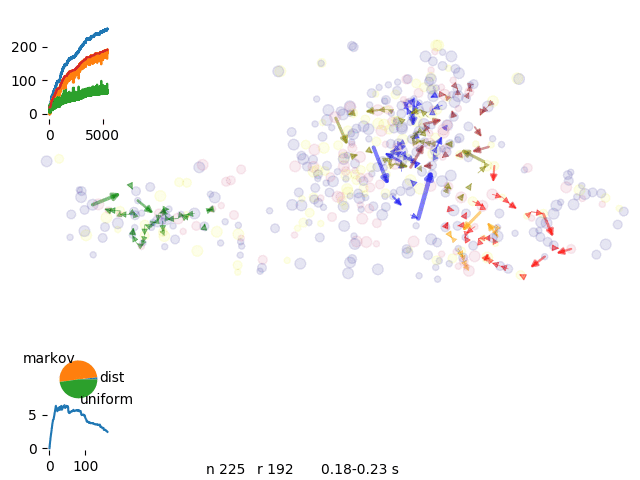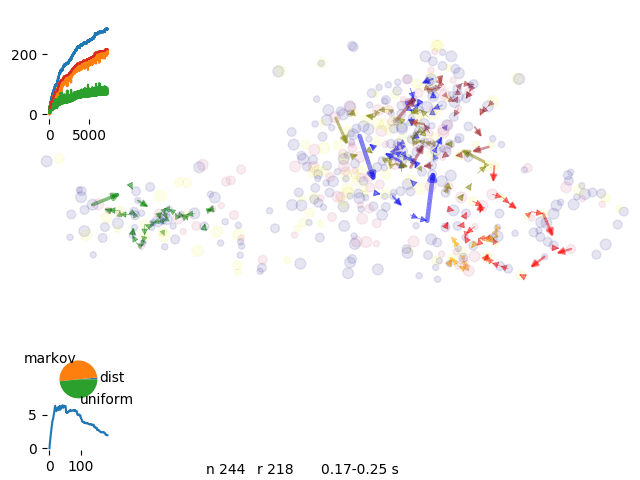
single spot move, solutions are a bit crowded

each driver start from a different k-mean cluster

distribution of the closest spot to a cluster

We have than a better separation of routes

single markov chain

energy evolution for single move engine

extrude, phantom, canonical

We define a series of moves to re-sort ants across the network

series of moves

For speeding up operations we introduce a series of moves to improve run time and convergency.

Extruding is suggesting a chain following the Markov Chain probability

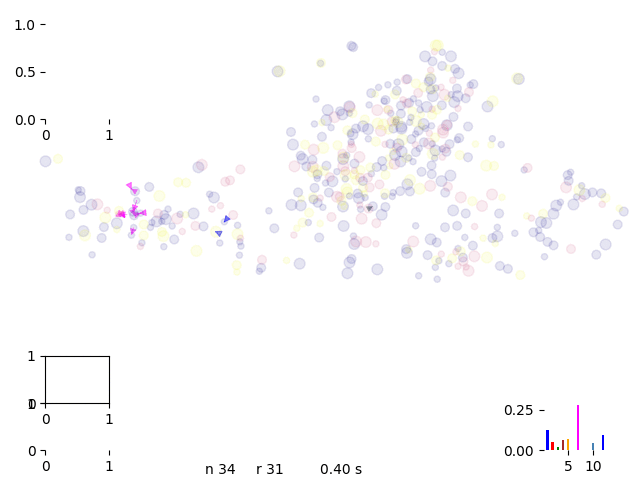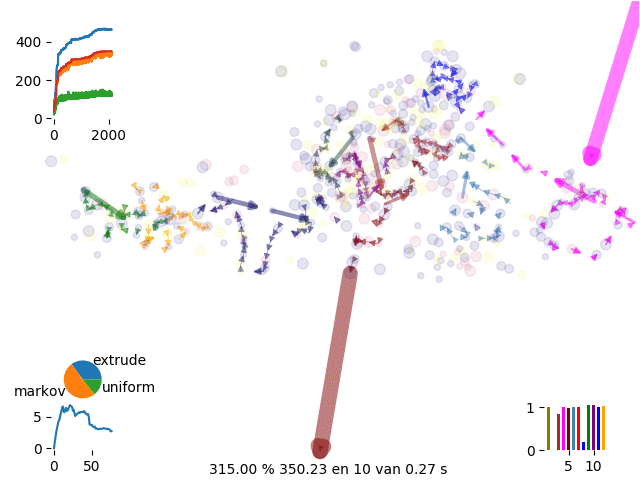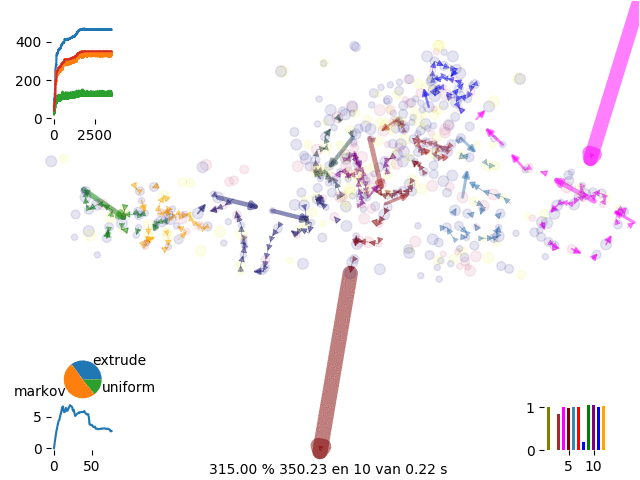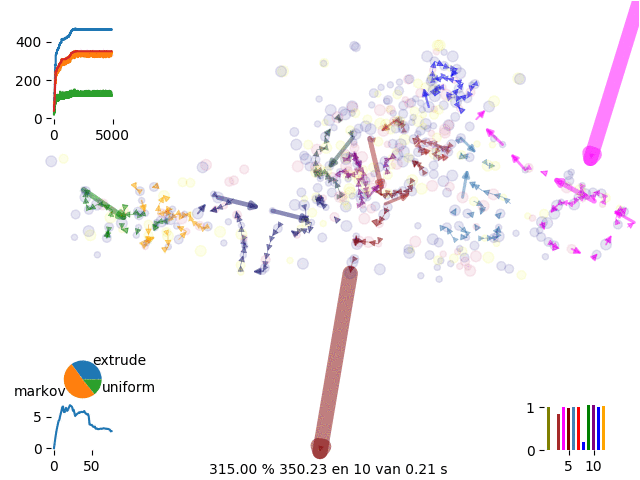
extrude move

With extrusion we dicrease calculation time to 1/10 getting to the same run time as routific.

We realize that sometimes some routes get trapped in a local minimum and we can’t get complete the occupancy of the van. Therefore we introduce phantom drivers so we have the option to discard uncomplete runs

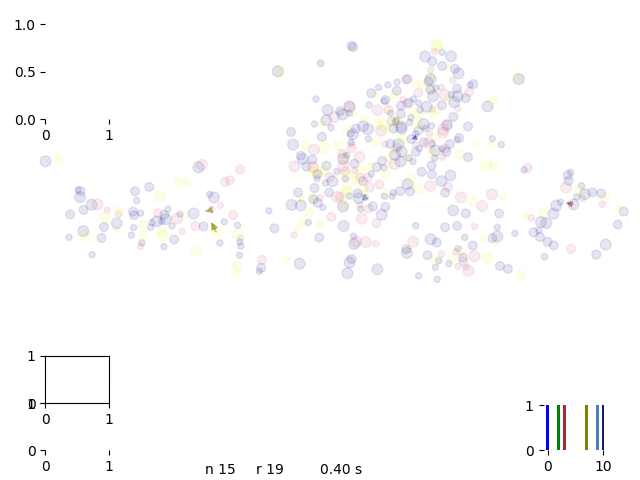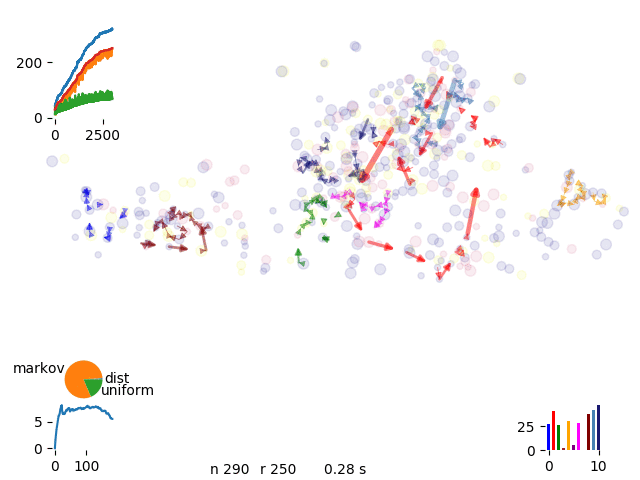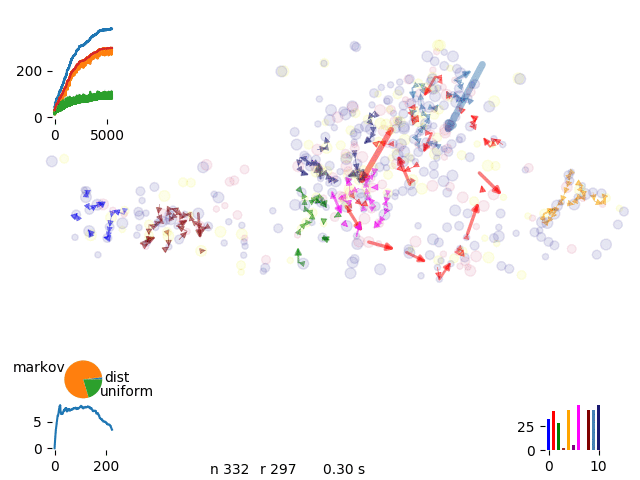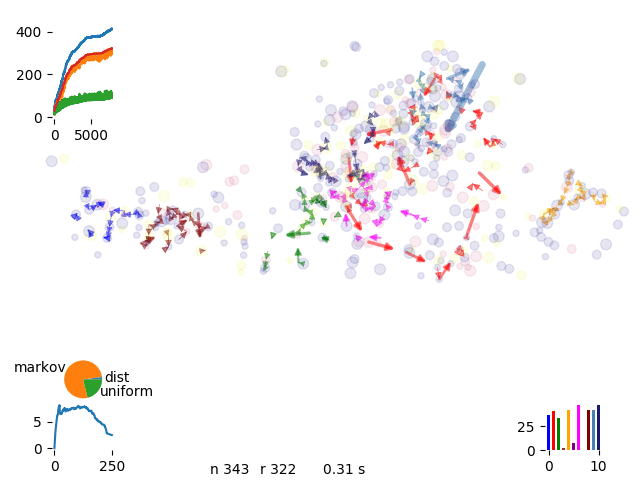
phantom move

Depending on the stage of the solution certain solutions are more appropriate than others

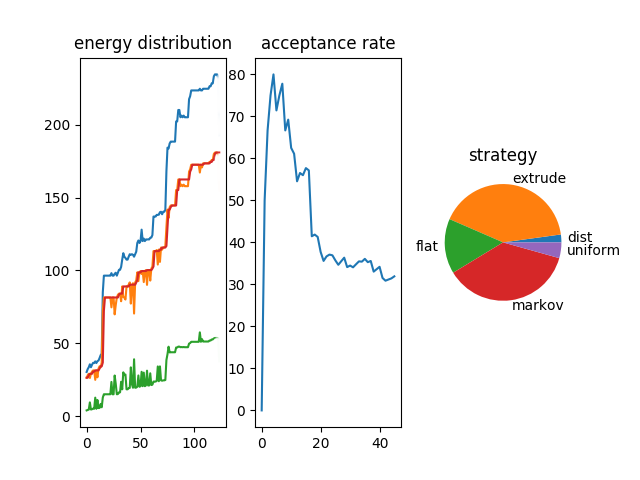
energy distribution for canonical simulations

To further improve convergence of solution we move to gran canonical simulation where we continously introduce and remove routes until we get to the best complete solution

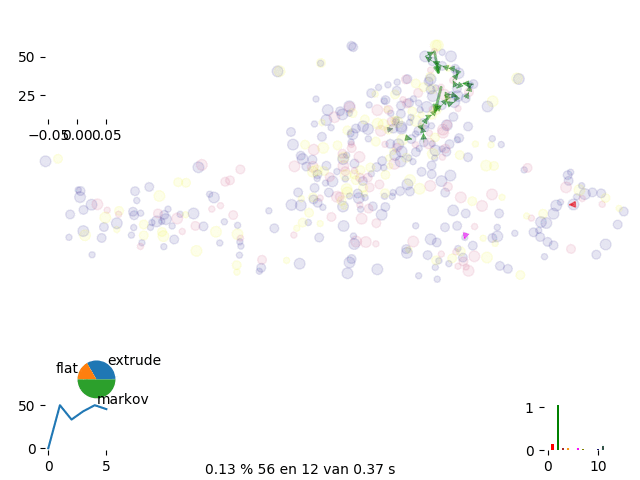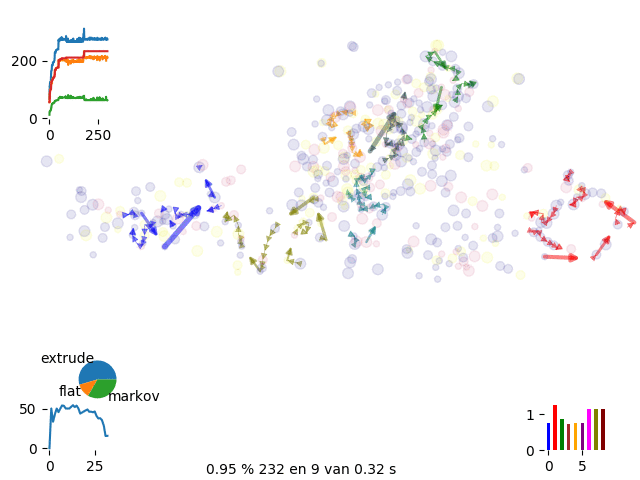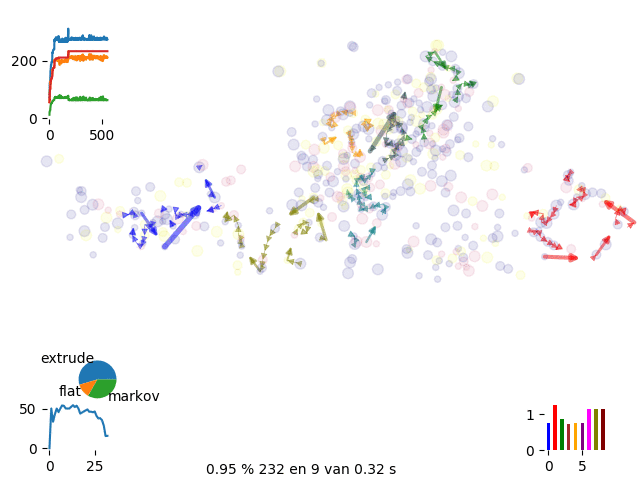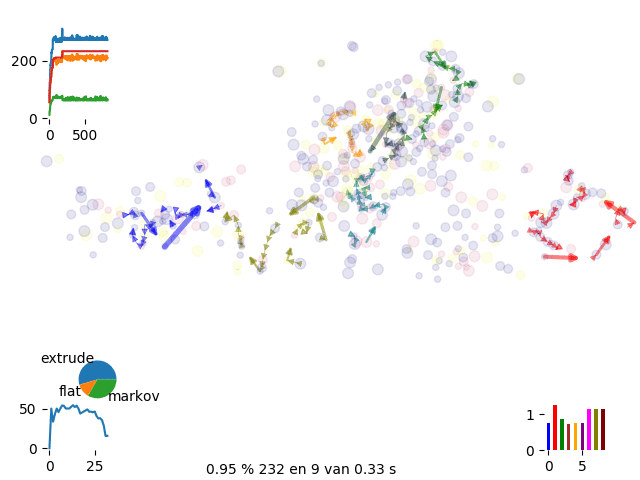
canonical move