building a graph

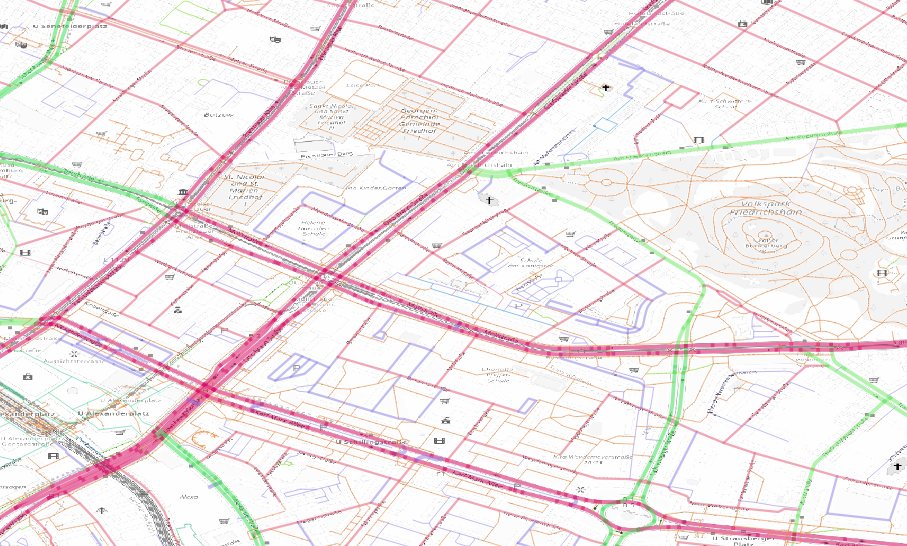
We can download the street network from openstreetmap and the information are pretty detailed

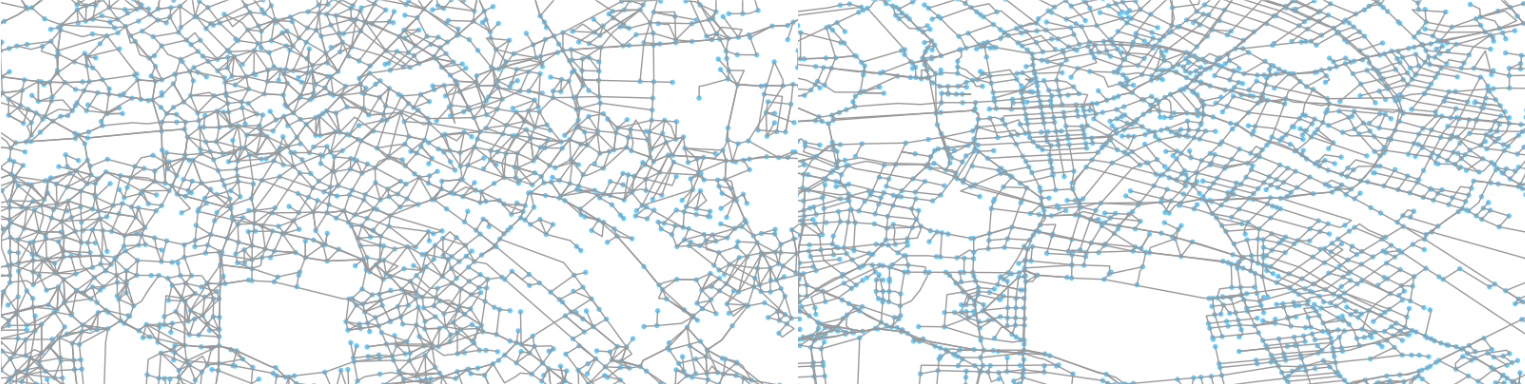
detail of a graph

We see a lot of different street types, depending on the mean of transportation we need to run some operation on the graph and reduce the number of edges keeping the correct distances.

• download the graph (berlin: 162k edges, 147k nodes) (643k segments, 526k nodes)
• select the routable street classes (32k, 30k)
• simplify the graph (24k, 23k)
• take the largest connected subgraph (17k, 11k)
• project the graph
• weight the graph

depending on the mean of transportation we select only particular street classes

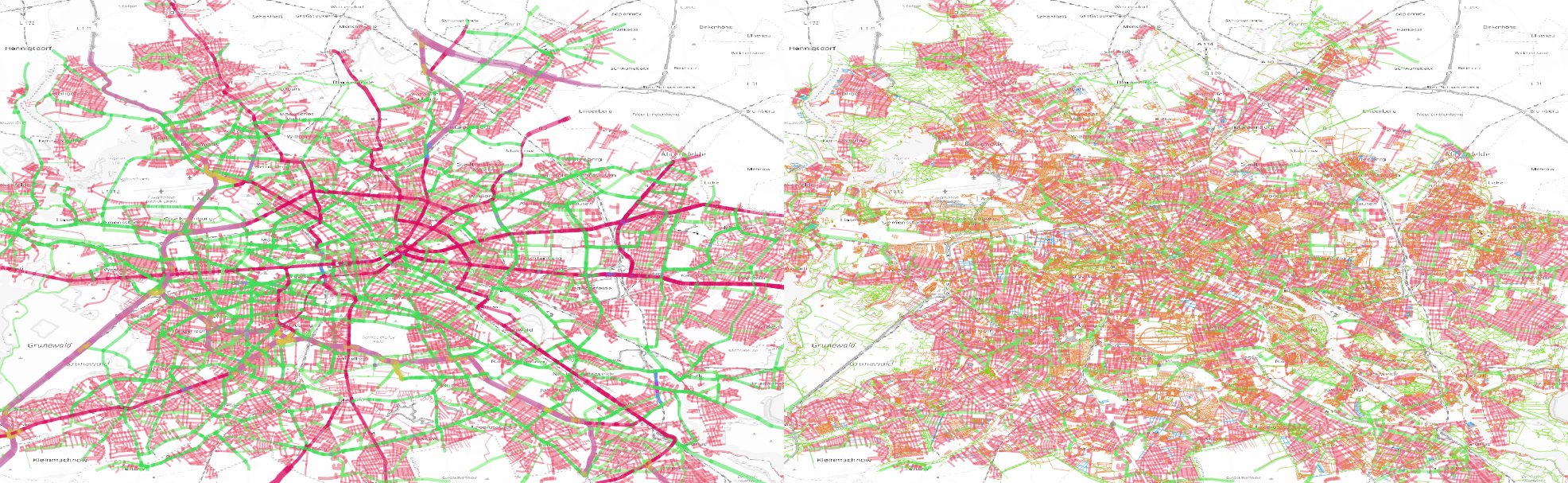
different kind of graphs depending on the mean of transportation

We build a graph from the geo dataframe

detail of a graph

We label the nodes with geohash and depending on the digit used we have different number of nodes and connectivity

With low digit we complete distort the geometry, with high number of digits we lose connectivity

disconnected graph

We realize that some parts are disconnected and therefore we take the largest connected graph

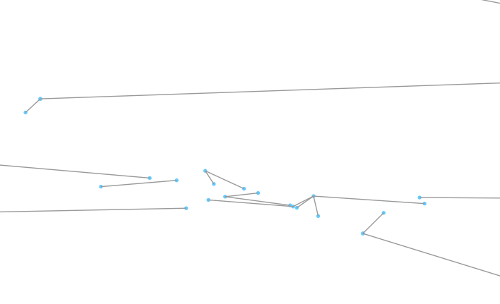
disconnected graph

We weight taking in consideration speed, street class, and length. We apply a factor for each street type

We can than weight a graph with this simple formula:

$$ \frac{speed * type}{length} $$

and obtain a weighted graph

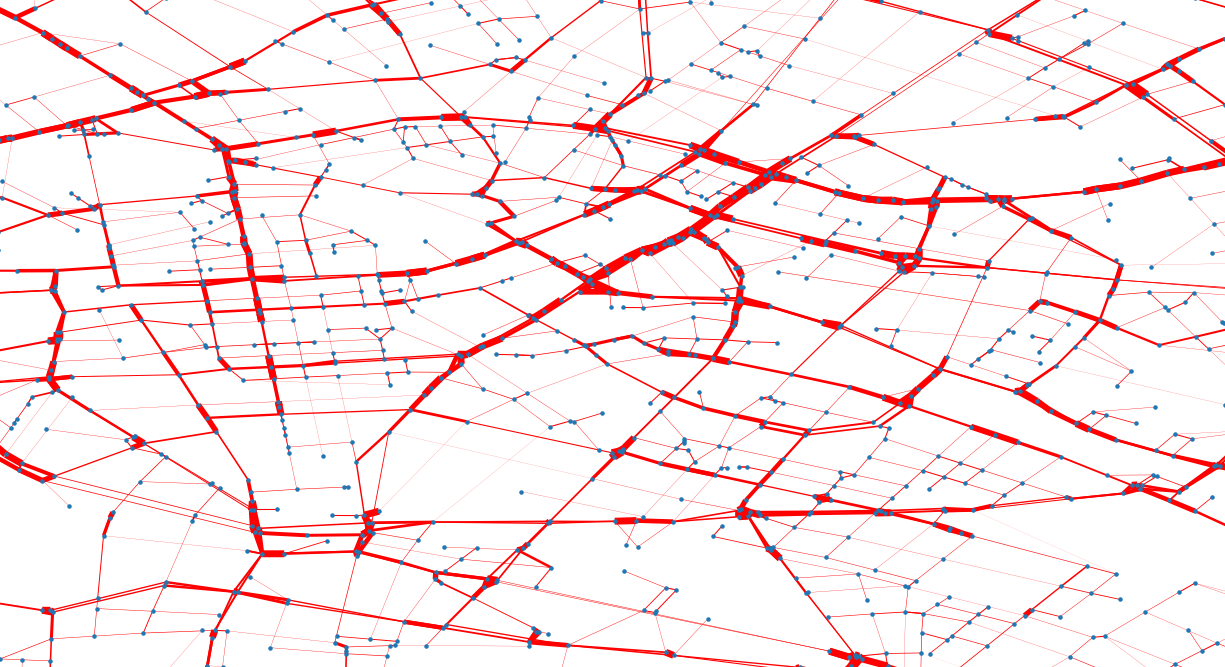
different weighting per street

calculating distance matrix

We selected the closest node per each spot

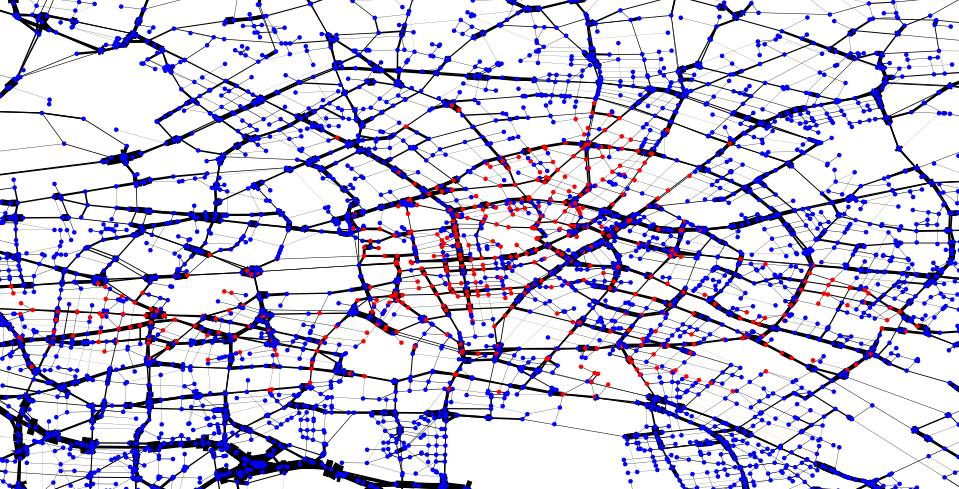
closest node per spot (in red)

The first iterations show not logical routes which is mainly due to the direct nature of the graph

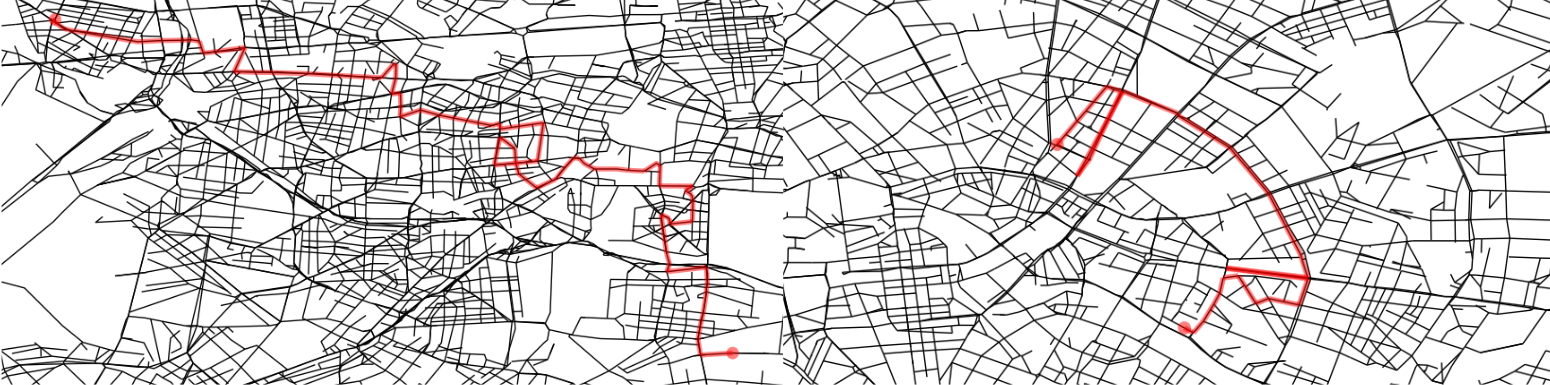
shortest path between two spots in a directed graph

A good directed graph is a lot of work and we by now use a undirected graph for reasonable routes

shortest path between two spots in a directed graph

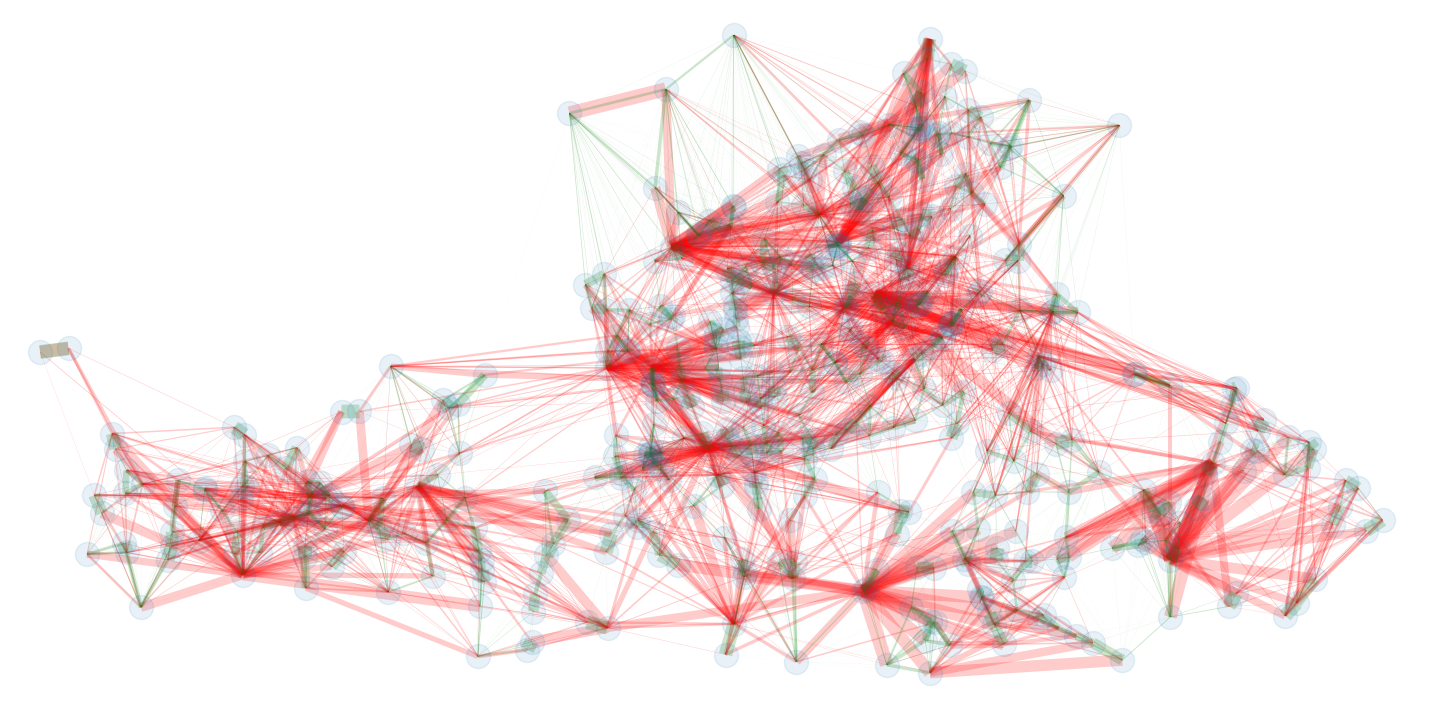
changes in the Markov graph moving to weights

We compare different graphs

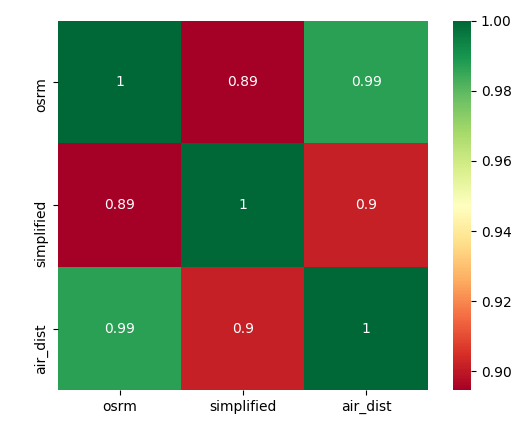
asymmetry matrix

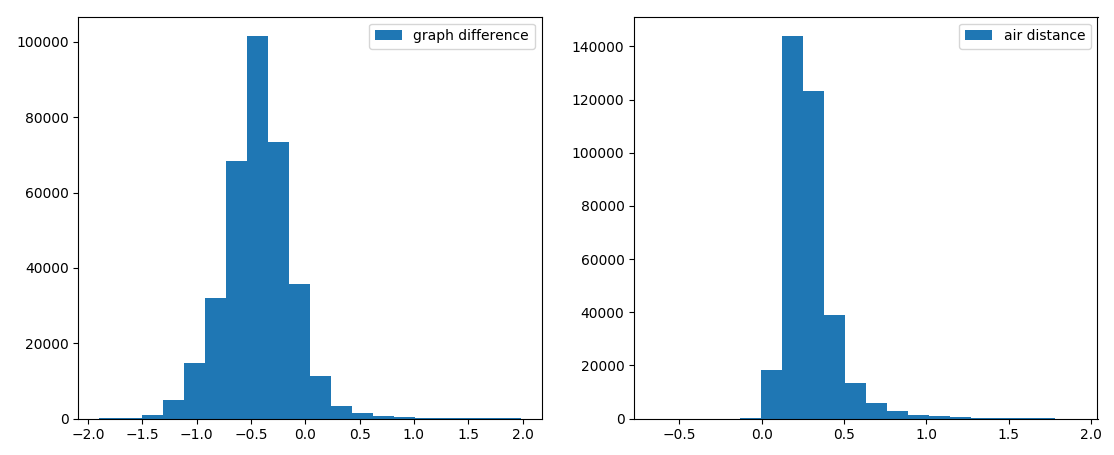
asymmetry distribution