painting with ML painting with ML
We can construct a class of encoders to transform pictures deciding what transformation we want to have as input and what as output.
The model is a gan as per ref, ref1, ref2, ref3, ref4, ref5 and further described down below
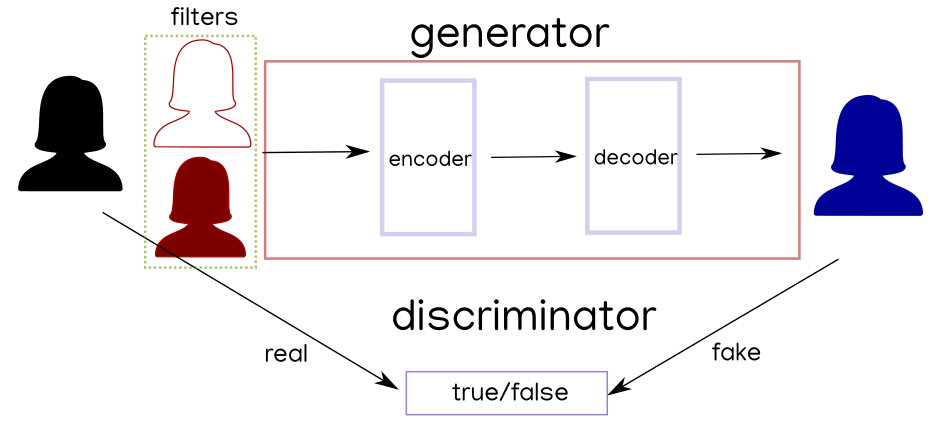sketch of the gan
We first take a bunch of pictures with people on it.
I ragazzi di via Panisperna
We use opencv to detect faces with Haar cascades and we cut and reshape pictures to the size of 360x480.
Face detection and rescaling
Haar cascade is faulty, one face is not correct, the eyes cascade is even worse
Faulty eye cascade
For each picture we run a routine to collect metadata and apply different filters:
series of image filters per image
In the following we run multiple sequences of training to realize different type of encoders
First we run an autoencoder (same picture as input and output) to see whether the generative network is good enough to describe the final result
visual result of the autoencoder
The finaly picture is a bit blurry but fit for the purpose
First of all we realize our pictures are gray but we want colors. The first transformation we apply is to take a set of pictures and train a model from the gray version to the colored one.
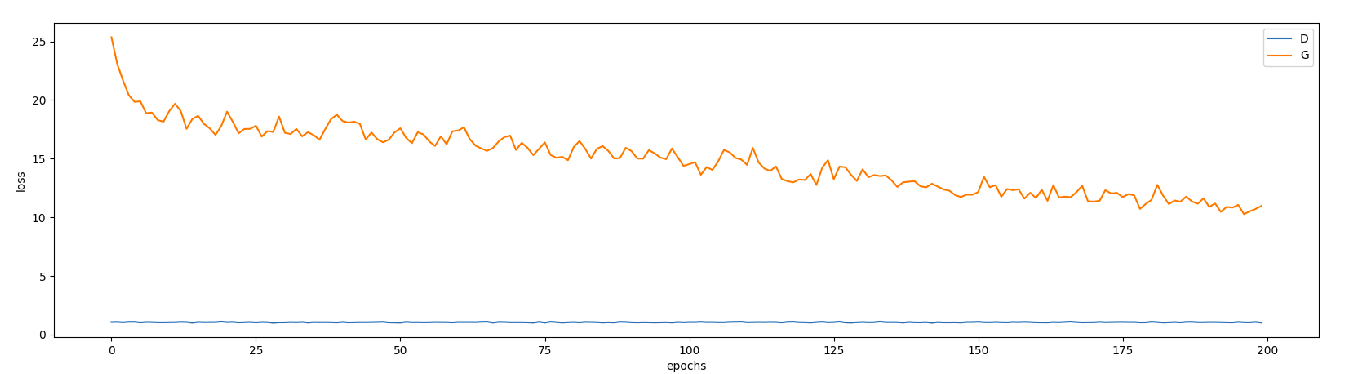train history for the gray to color
transformer
We run the gray transformer to 200 epochs of 64 batches each.
So we can finally color the b/w pictures
black and white pictured colored
We apply 3 rgb binary layers and learn the encoder towards the original picture
outputs of the color binary encoder
In this case we add 4 contours per color using 50,100,150,200 as thresholds. We see at first that the contours are pretty visible
first batches of color contour
transformation
After few hundreds of epochs the effect is nicely smoothed out
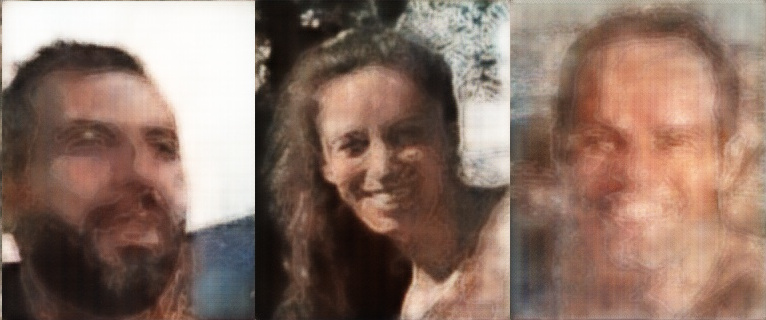late batches of color contour
transformation
A Canny filter doesn’t provide enough information as input
first batches of Canny contour
transformation
After many epochs the results are still poor
late batches of Canny contour
transformation
We take different subsets of people and compute the average face/expression morphing every picture into another one in the same subset
The outcomes converge to an overall average
After few iterations all results look the
same
We use as input random noise and see what the model has learned as pure generator
Here is a gallery of notable outcomes from the generators.
Gallery of notable faces
The model is a gan divided into a discriminator and a generator which is designed as a autoencoder with different convolution layers
An autoencoder is defined by an encoder and a decoder which are used for image compression and decompression.
An encoder reduces the dimensionality of a picture trying to extract the most relevant information without losing the essential features of the picture. The decoder works in the opposite direction because an encoded picture won’t be intelligible.
The encoder is made of different layers where each comprise the local information into averaged pixels. The typical operation is a convolution which convolutes different kernels on a correspondent pixel square (usually 3x3) times the color channels. A cube of 3x3x3 after convolution is represented by a single pixel and the next cube is analyzed moving by few pixels (called stride, usually 2x2).
The subsequent layer can be a pooling where the image is downsampled, usually with a maxpooling which is taking the maximum value within the square downsampled.
We introduce additional layers to perform some regularization such as batch normalization to provide a proper scale to the batch in use. Another important habit to prevent overfitting is to use dropout randomly removing connections from the neurons.
The discriminator works as an encoder until it flattens into a categorical axis where to each category a probability is assigned.
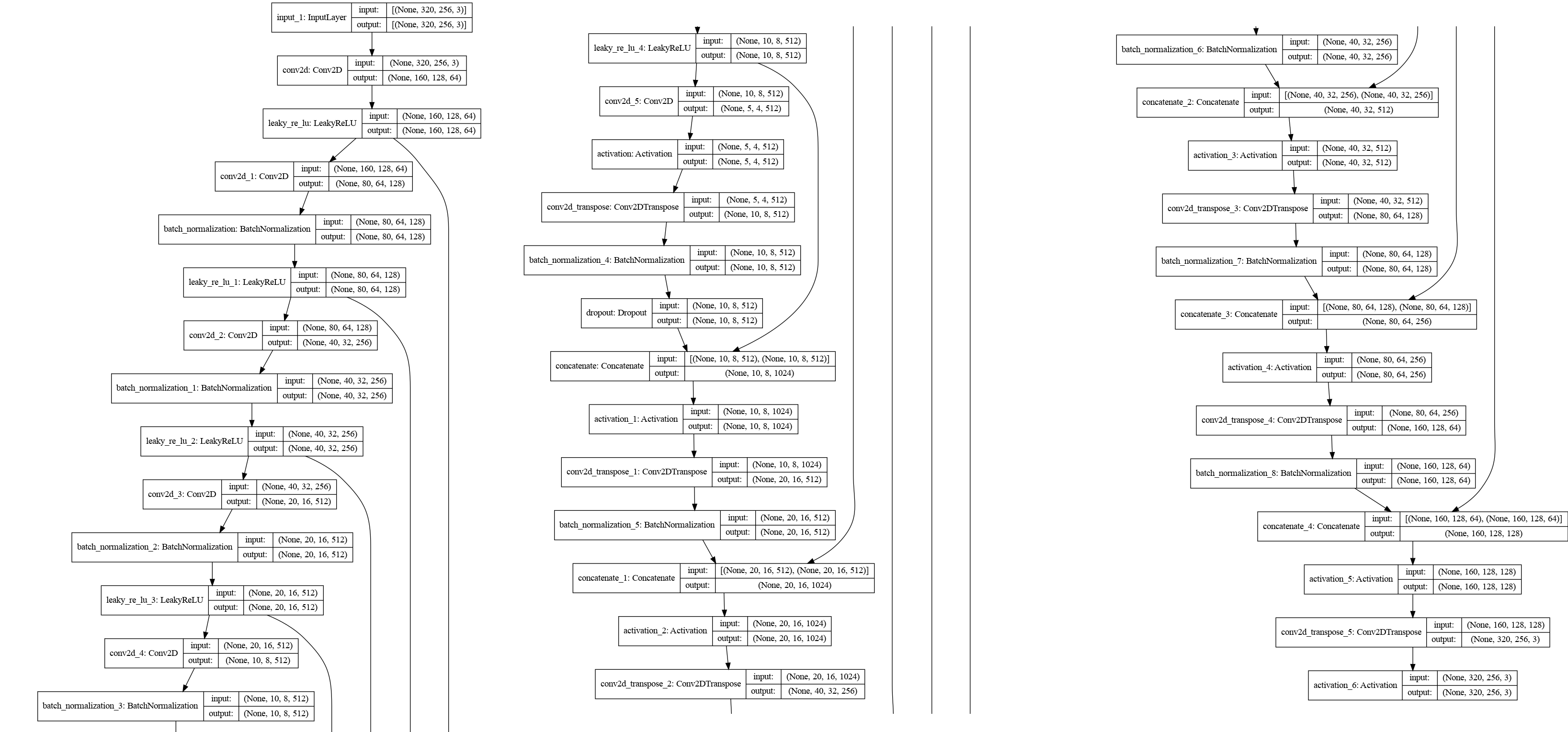sketch of the generator model
The discriminator takes the image as input and quatify the fakeness of it
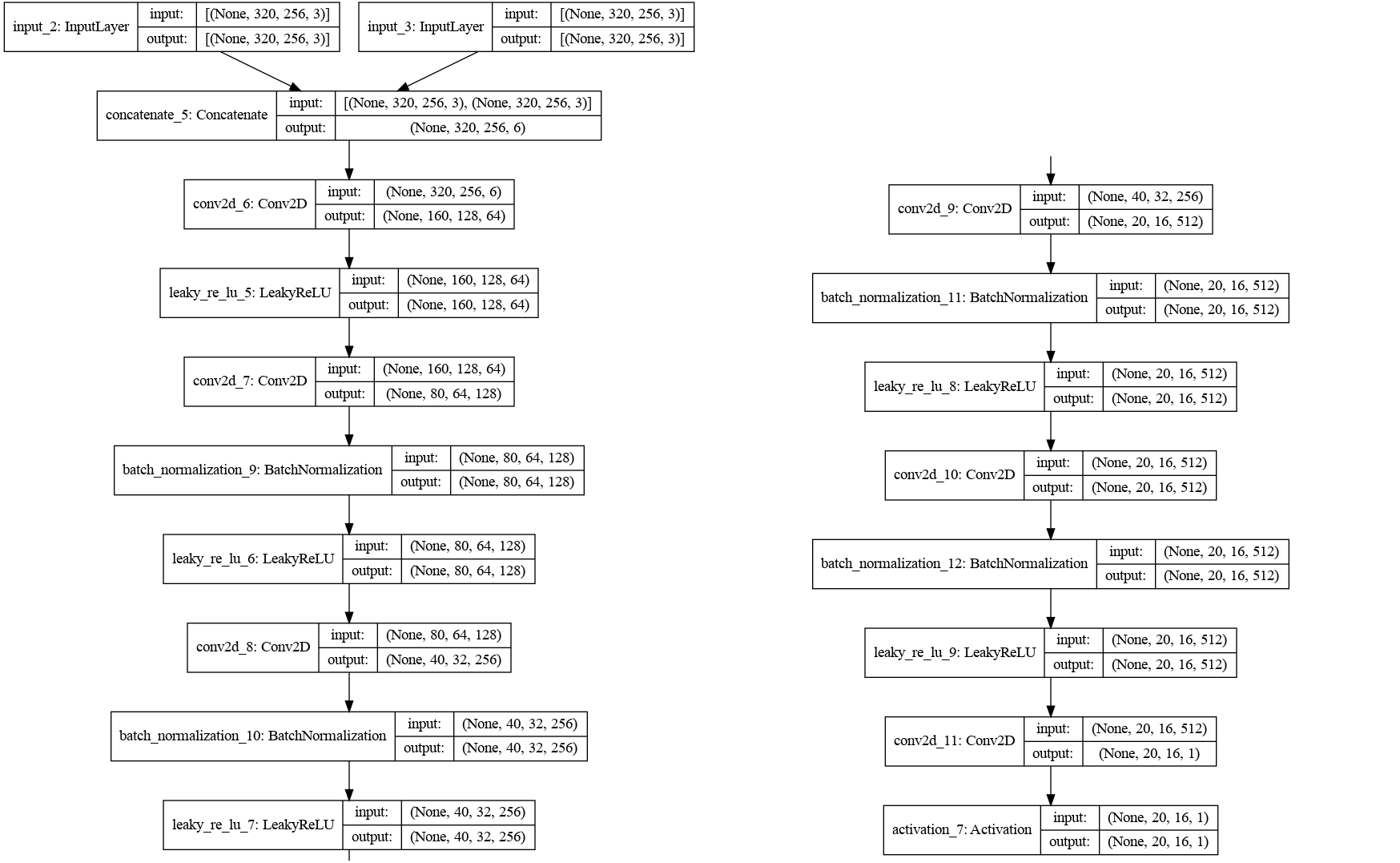sketch of the discriminator model
The gan combines the generator and the discriminator in an adversarial fashion ref
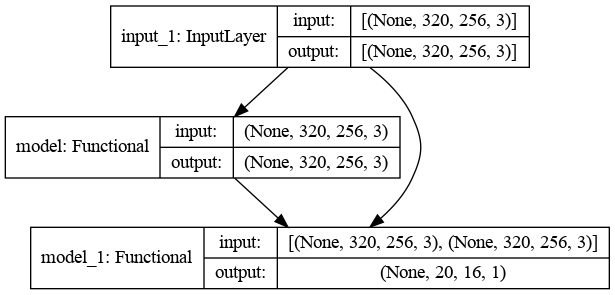sketch of the gan
All the pictures have been resized to 256x320 which is not quite 3/4 but it contains many powers of two (2^8 x 2^6*5) and allows our network to go a bit deeper with the convolution.
