Antani

Ant - agent/network intelligence

ants optimizing paths on a network

Efficiency

Why operation efficiency?

• Fill the gap between revenue and cost
• Think as a network, not single operator
• Select the most valuable tasks

Problem

The closest path facing the warehouse fullfilling the most valuables tasks

optimization engine requirements

• Focus on profitability
• Plan shifts
• Consider task time and revenue

Commercial softwares?

Delivery based, routific: * Long deviations * Skipped tasks * Unclear priorities

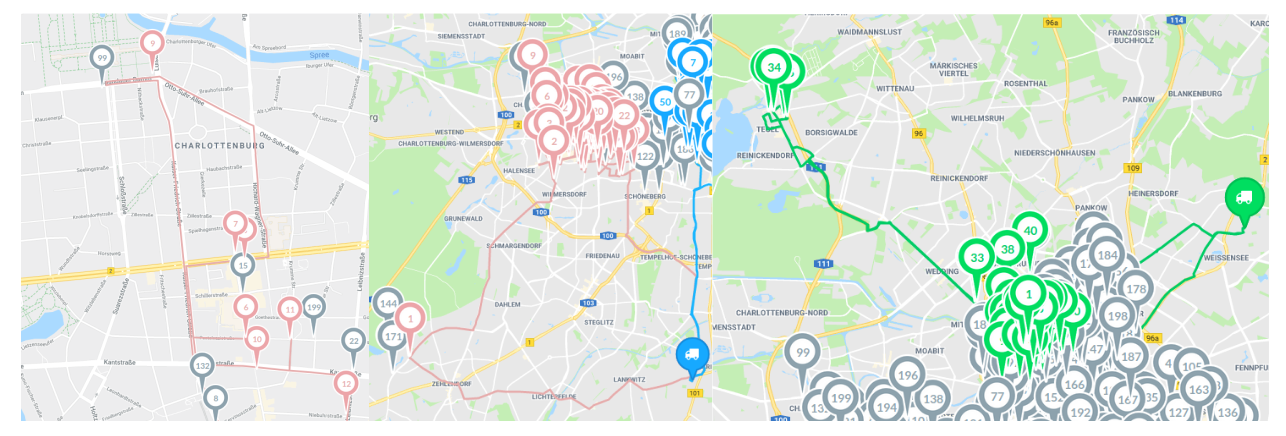
problems with routific

No resuming, everytime a new simulation

Google or-tools?

open source software suite for optimization

or-tools solutions

Many crossing Incomplete vans, long trajectories:

• incomplete solution (-20%)
• job to be killed
• 0.5-75mins

In house solution

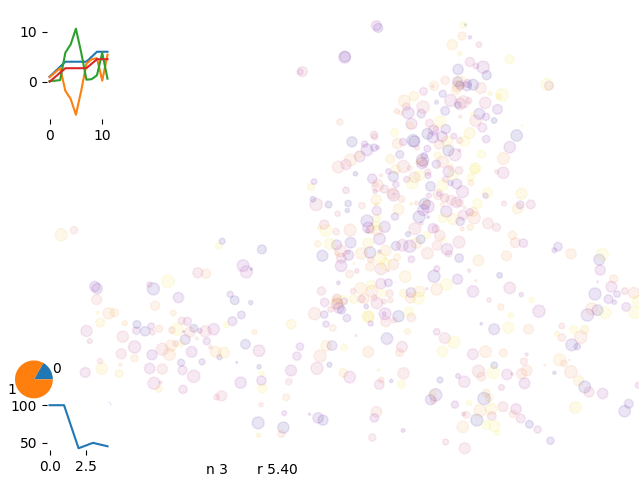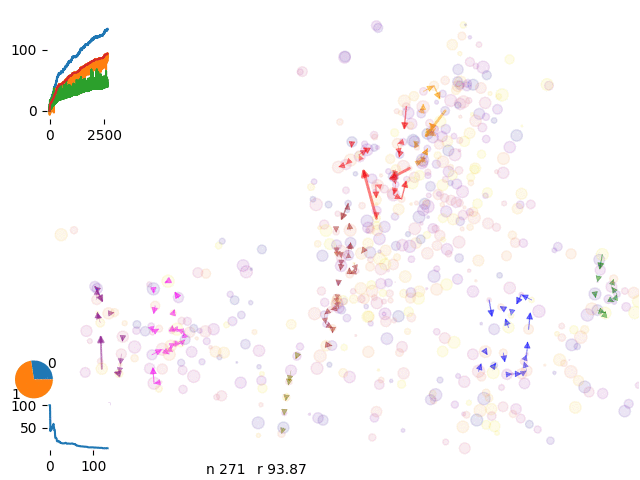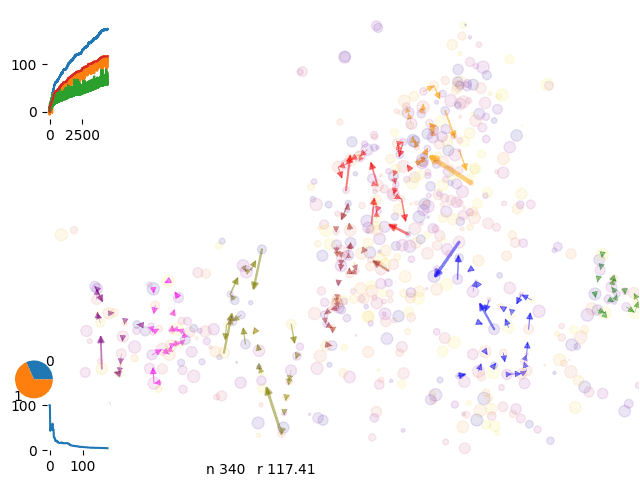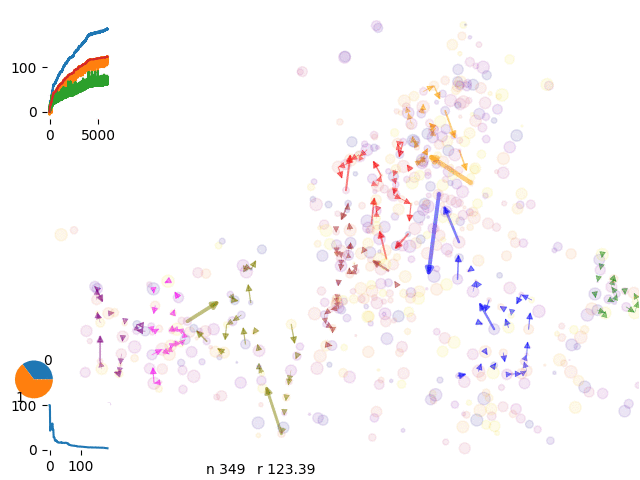in house optimization engine

Step by step task assignement

Path optimization

Path like polymers

PhD defense – computational biophysics 2012

Optimization engine

Ludewa/Tanzania - 2013

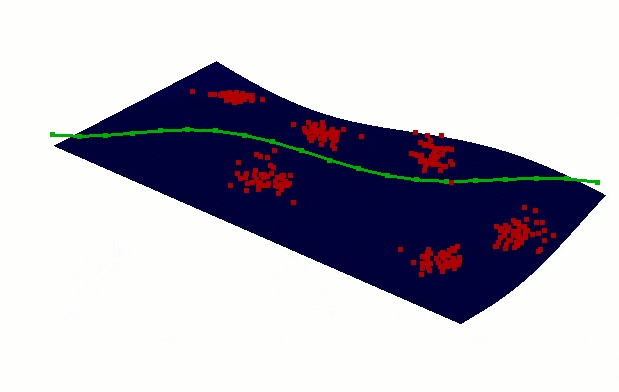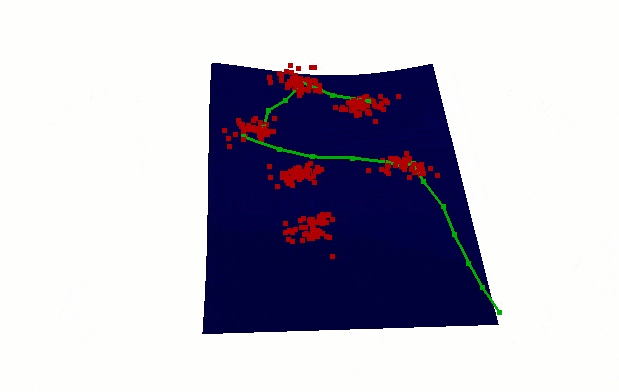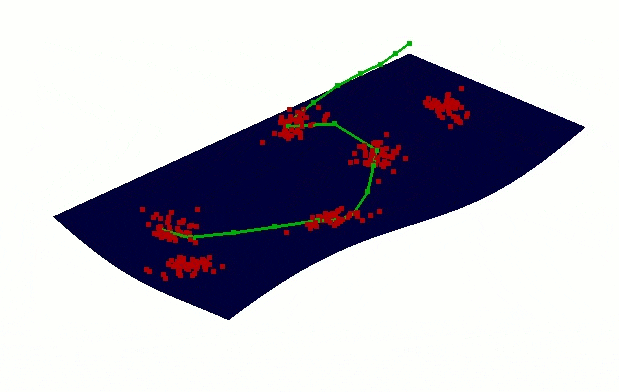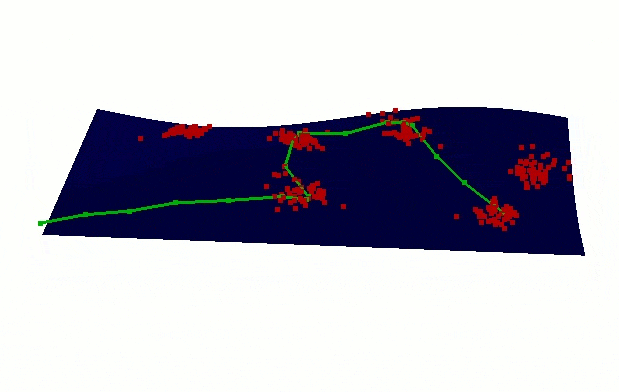
Electrical line design to connect households to the new power plant

Building a graph

From detailed street network to an efficient graph

Subset, connect, simplify, subgraph, check directions…

weighting

Weight every segment

Maxspeed, streetclass, length, junctions

Graph setup

Checking routes

checking routes

Good correlation between spot2spot routes in graphs and air distance

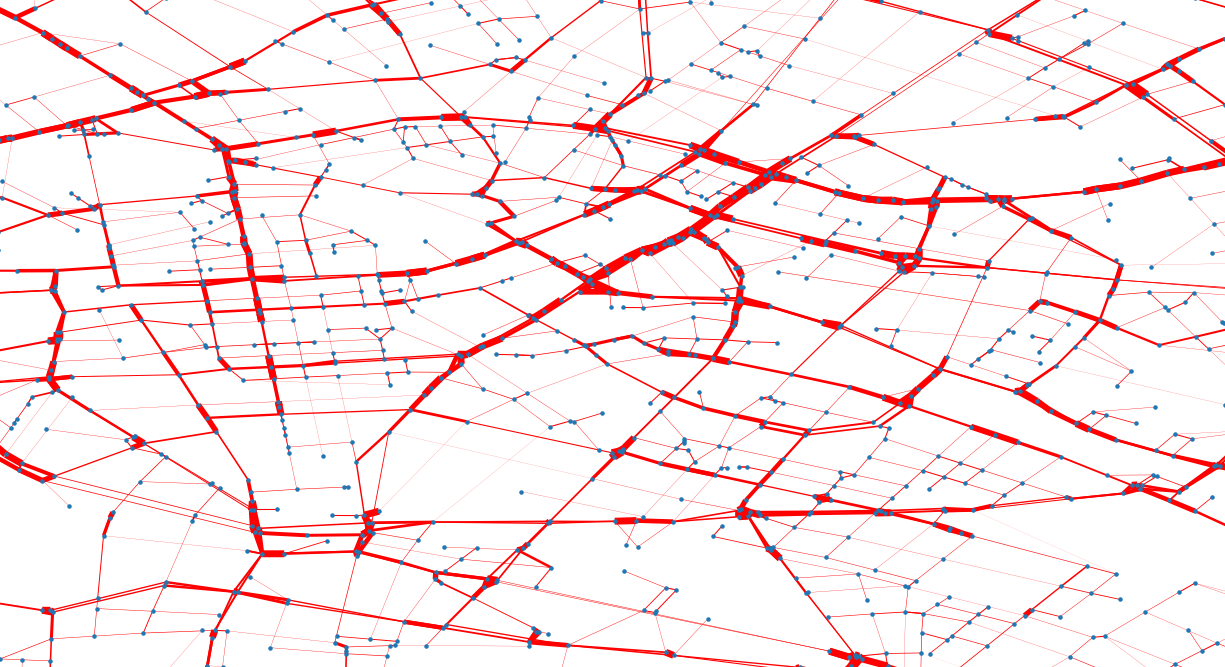
Osrm – open street routing machine

Routes

Subset the city in geohashes (~70m)

routing information

Calculate all pair distances and build a lookup database

pair relationship database

Tasks

Sum up tasks in the same geohash

graph edges kept

Keep only neighbor connections between tasks

Sense move reward

Ant/colony

an ant per loop, iterate over the network

energy definition

Energy: * +separation * +task value * - area * - task time * - tot distance

Path/network

An ant connecting each task

antani concept

Path opt

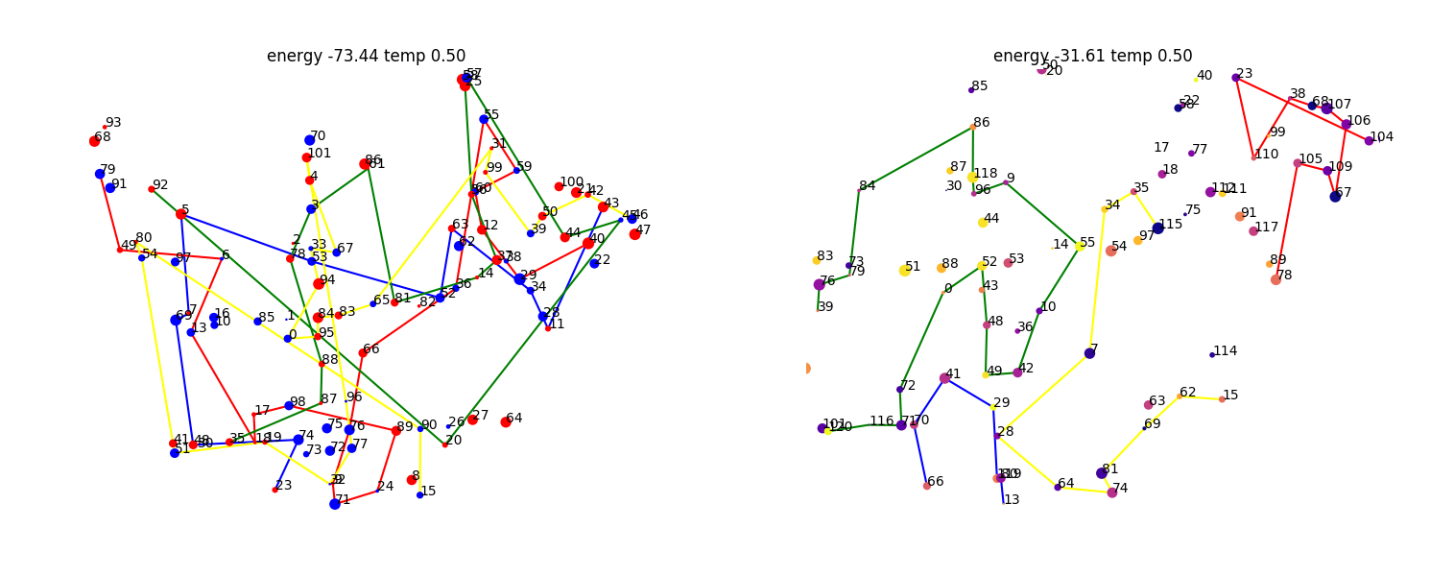
optimize sequences

Monte Carlo

Single random move

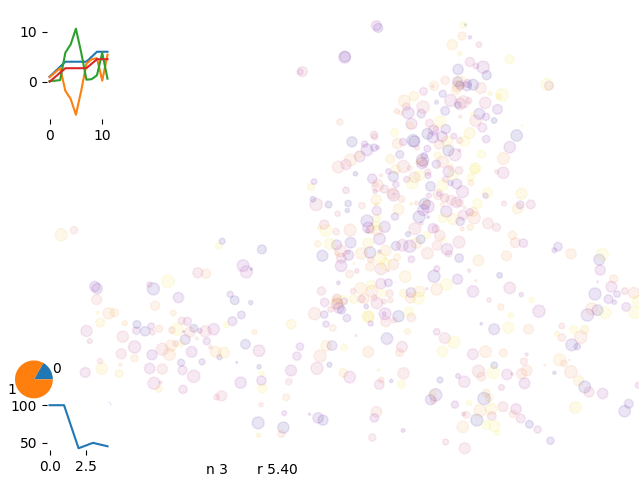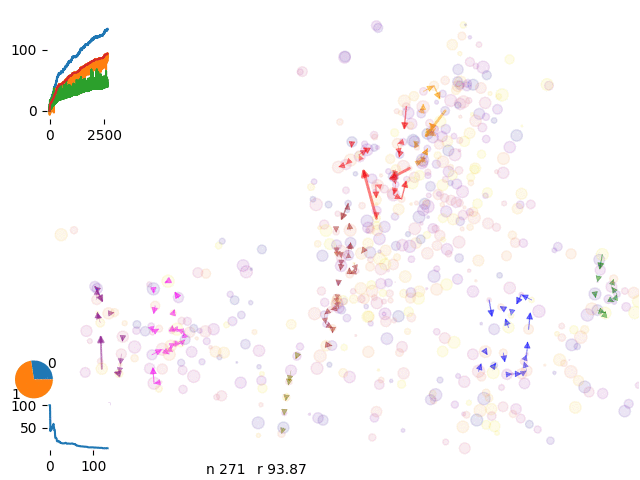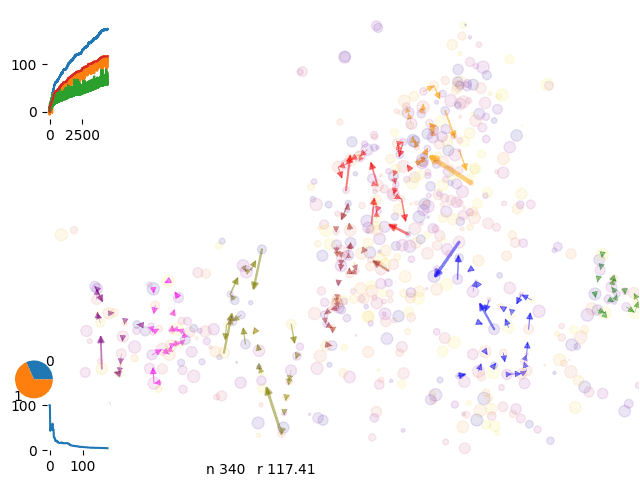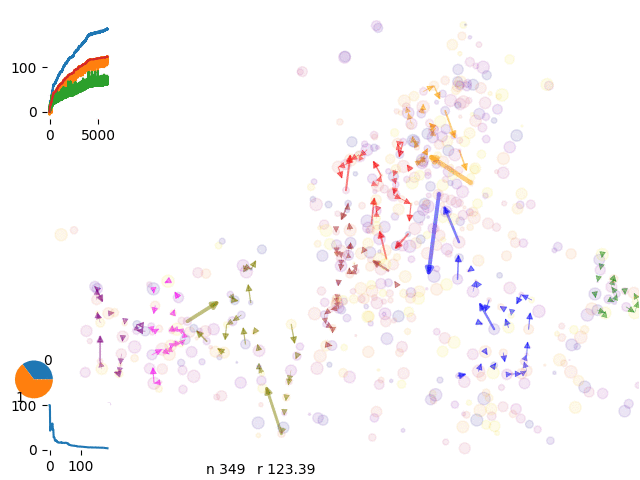
energy evolution

Asyntotic energy and move acceptance rate evolution

Markov Chains

Transition probabilities, limit links

markov chains

We limit the possible moves leaving the most probable

Enhance moves

single, Markov, distance, extrude

move selection

Spot selection according different probabilities

Simulation boost

• Faster convergency
• Higher acceptance

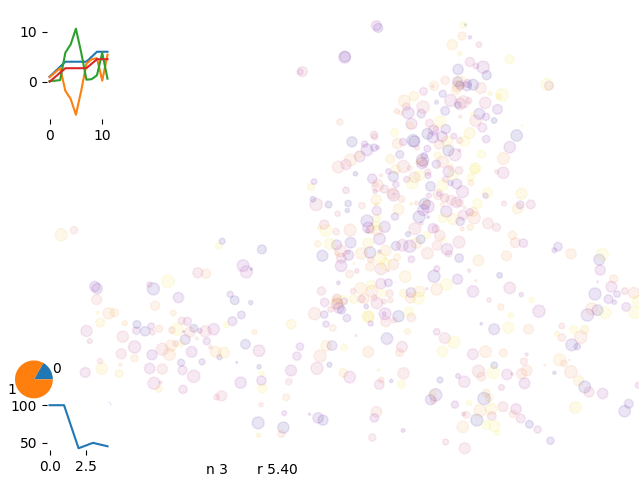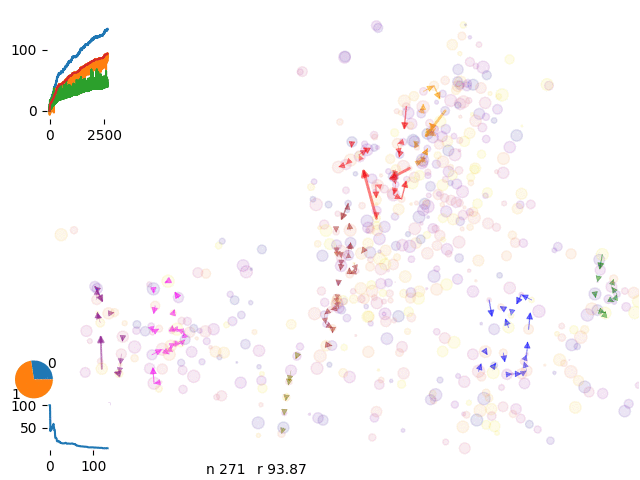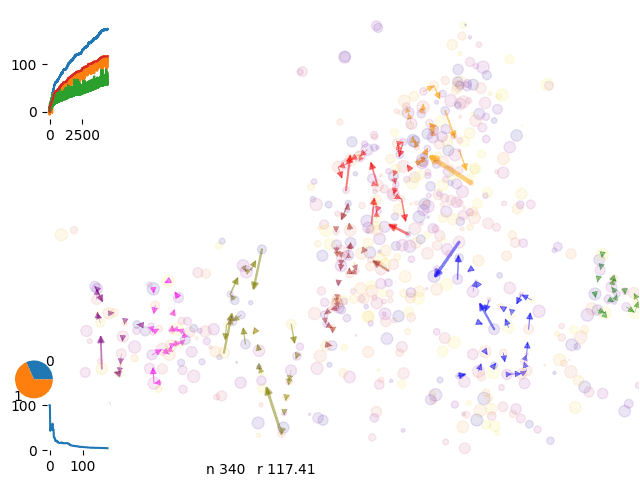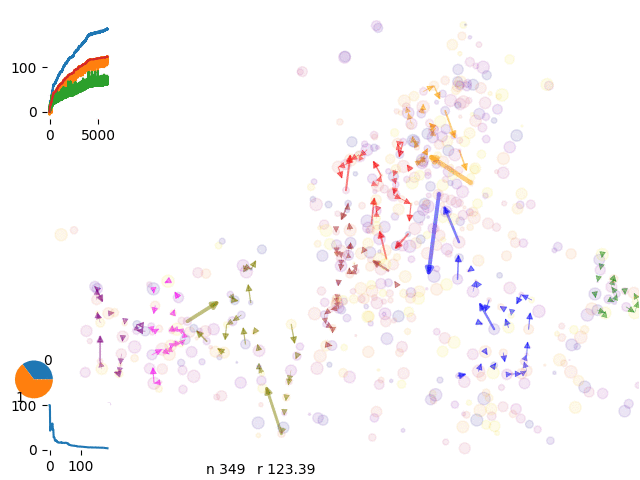
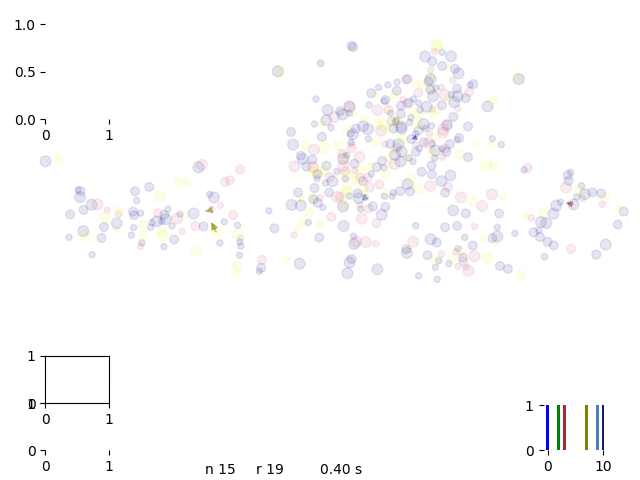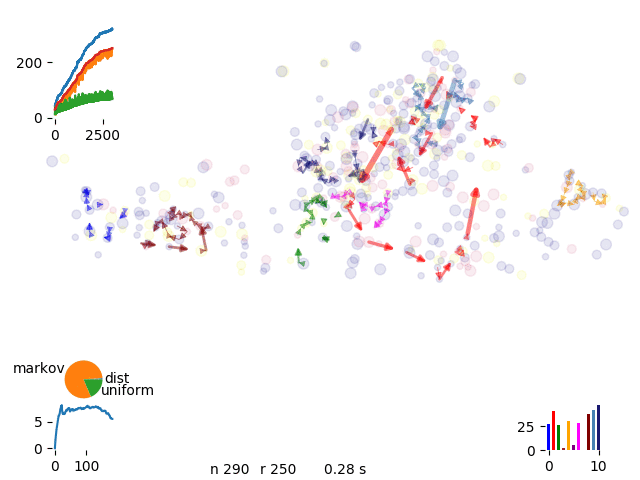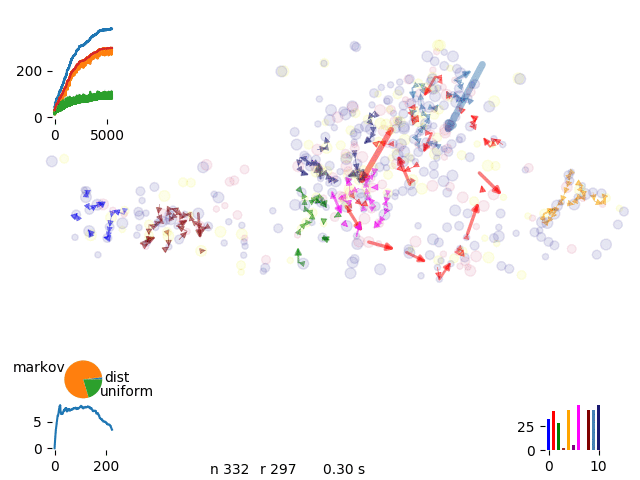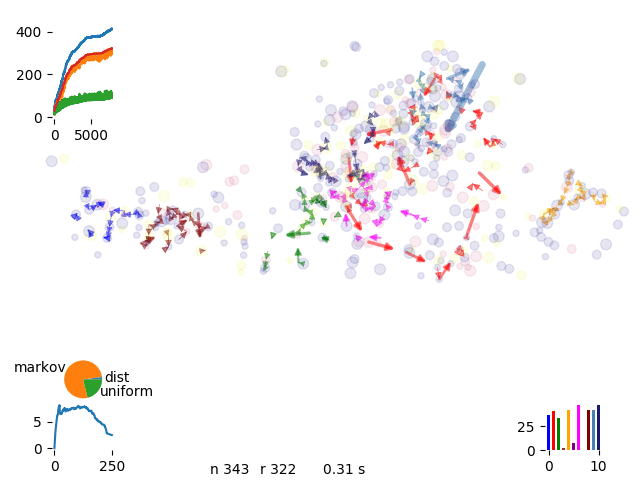
Single move, routific optimization, Markov chain, extrusion, grand canonical…

Calculation time

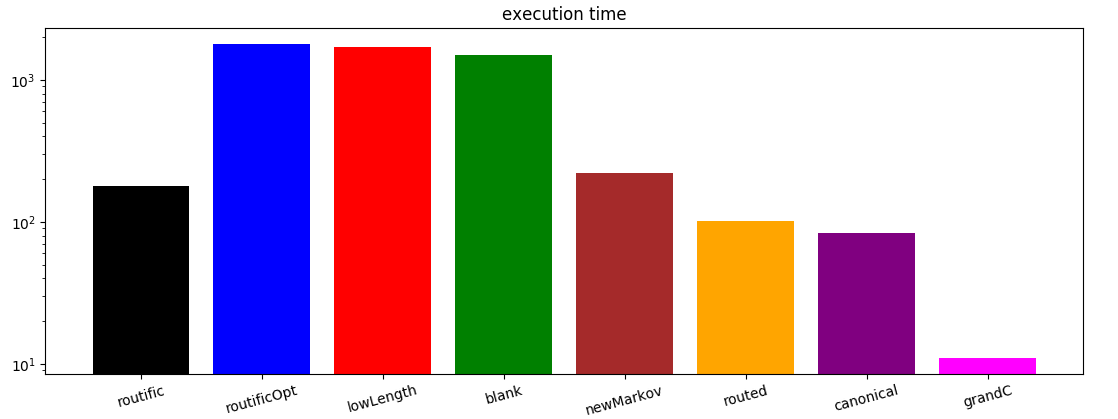
Early simulations were too slow

Find a score:

scoring

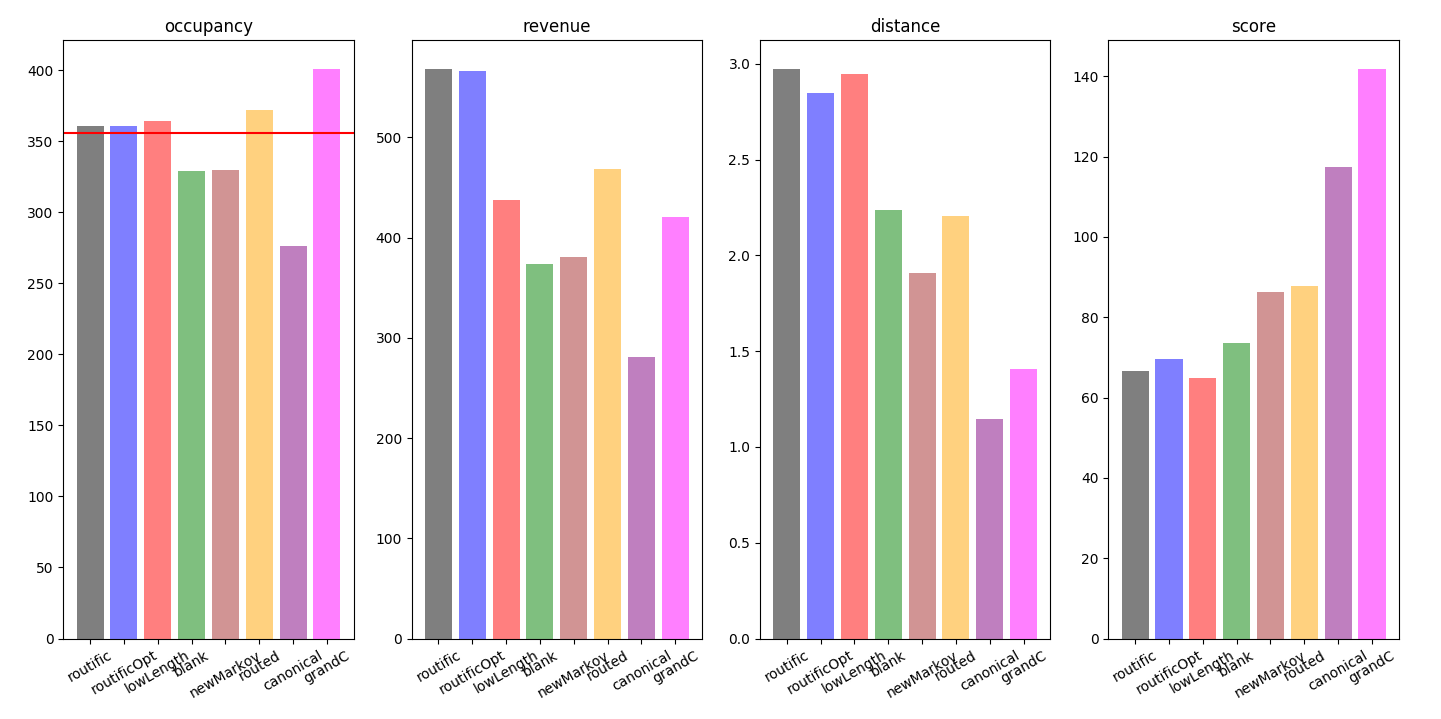
kpi comparison

+completion + revenue – distance - time

Reinforcement learning

Improve acceptance

reinforce moves

Single agent reinforcement is too slow and chaotic

Posterior probability

Improve with real data

posterior probabilities

Demand

demand forecast

Microservice design

Backbone +microservices

engine design

Asynchronicity

Docker, flask, redis,celery

antani infrastructure

Client – broker/worker design

Frontend

OpenLayers, d3, ajaxDocumentation

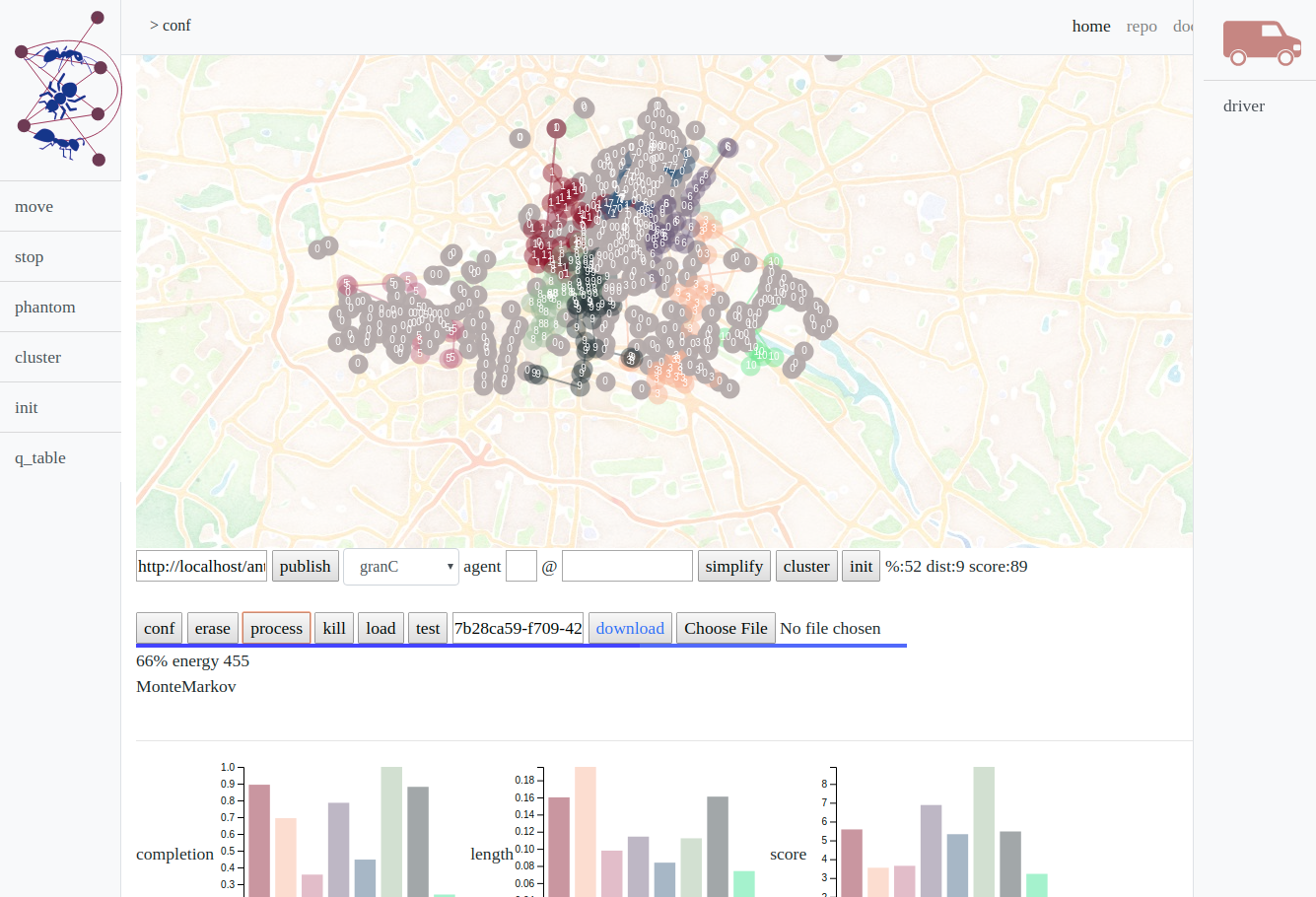antani frontend

Documentation

module mallink

Code

library ecosystem

…started in 2006

Outlook

• Ready for spring
• Drivers feedback
• Process real data
• Compare with rideos
• …

Summary

• Start, stop, resume
• First draft within few seconds
• Clear operating areas
• Weighting potential revenues
• Focus on profitability

Acknowledgement

Circ – fleet engine team Carlo Mazzaferro – productization of antani

Theory

Gibbs sampling

We describe a probability distribution via its moments μ⃗

p(x⃗;μ⃗)

We have a system x⃗ where each x is in a certain state s. We define a energy function which depends on the states of system and a set of parameters θ. In our case the system is a series of field tasks on a map and the state is the agent who is fulfilling the task.

The energy of the system is the sum of the revenue per task minus the cost: task time and path length. The parameter set θ defines the revenue and cost factor + external factors (temperature T, traffic time h,…). Ideally we will express the parameter set in terms of external factors θ(T,h) or change the metric (distance) of the system d(T,h)

E_a(x⃗|θ) = n_s ⋅ r_s − c_d ⋅ d_a − n_s ⋅ t_s

where n_s is the number of spots, r_s the total revenue per spot, t_s is the total operation time, d_a the distance of that agent.

The probability distribution for a certain state and parameter follows the Boltzmann distribution

$$ p(|) exp(-E()/kT)

Target probability distribution

$$ p(\vec{x}) = \frac{w(\vec{x})}{Z} = \frac{1}{Z} \prod_c \phi_c(x)$$

estimator

$$ \frac{1}{T} \sum_{t=1}^{T} \phi(\vec{x}) \qquad E_{p(x)}|\phi(x)| = \sum_x p(x)\phi(x) $$

From the state x⃗ we create a state x⃗′ where we create a sample x_j → x_j′, basically: x⃗′ = x₁, x₂, ..., x_j′, ..., x_n

$$ p(x) = \frac{exp(E(x)/T)}{Z} $$

$$ A(x'|x) = min(1,p(x')/p(x)) = min(1,exp(\frac{ E(x') - E(x)}{T})) $$

Bayesian statistics

We want to calculate the posterior probability doc which is the probability of a parameter set θ from a given state X

$$ p(\theta|x) = \frac{l(x|\theta)p(\theta)}{p(x)} $$

where l(x|θ) likelihood, p(θ) prior, p(x′|x) the probability to move from state x to state x′ and p(X) normalization factor

p(X) = ∫dθ * p(X|θ*)p(θ*)

The likelihood is about finding the momenta of the distribution for a given data set (usually via regression), the probability distribution is the theoretical distribution for the system (independent on the data acquired). In a correct sampling the two match.

proposal distribution p(x) - target distribution g(x) p(θ|X)

Step increment θ′ = θ + Δθ

$$\rho = \frac{g(\theta'|X)}{g(\theta|X)} \qquad \rho = \frac{p(X|\theta')p(\theta')}{p(X|\theta)p(\theta)}$$

sampling from probability from a state x doc

xπ̃(x)

High dimensional computing (over all states)

c = E[f(x)] = ∫π(x)f(x)ds

optimization

x *  = argmaxπ(x)

Learning and Bayesian hierarchical modeling for a given parameter set Θ

$$ \Theta * = argmax l(\Theta) ; l(\Theta) = \sum_{i=1}^{n} log p(x_i;\Theta) $$